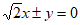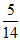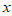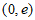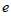本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 抛物线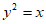 的准线方程是
的准线方程是
A. 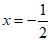 B.
B. 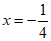 C.
C. 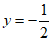 D.
D.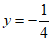
2. 在复平面内,复数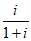 对应的点位于
对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 在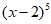 的展开式中,
的展开式中,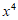 的系数为
的系数为
A. 5 B. -5 C. 10 D. -10
4. 已知直线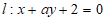 ,点
,点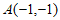 和点
和点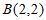 ,若
,若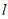 ∥AB,则实数a的值为
∥AB,则实数a的值为
A. 1 B. -1 C. 2 D. -2
5. 某三棱锥的三视图如图所示,该三棱锥的体积为
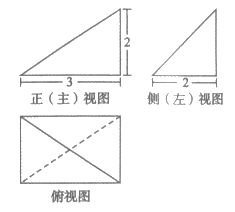
A. 2 B. 4 C. 6 D. 12
6. 已知向量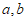 满足
满足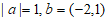 ,且
,且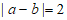 ,则
,则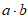 =
=
A. -1 B. 0 C. 1 D. 2
7. 已知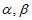 是两个不同的平面,”
是两个不同的平面,”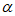 ∥
∥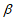 “的一个充分条件是
“的一个充分条件是
A. 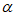 内有无数条直线平行于
内有无数条直线平行于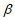
B. 存在平面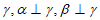
C. 存在平面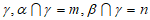 ,且
,且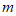 ∥n
∥n
D. 存在直线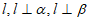
8. 已知函数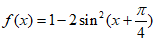 ,则
,则
A. 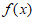 是偶函数 B. 函数
是偶函数 B. 函数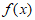 的最小正周期为
的最小正周期为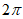
C. 曲线y=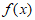 关于直线
关于直线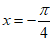 对称 D.
对称 D.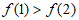
9. 数列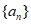 的通项公式为
的通项公式为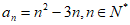 ,前n项和为
,前n项和为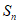 。给出下列三个结论:
。给出下列三个结论:
①存在正整数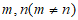 ,使得
,使得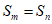 ;
;
②存在正整数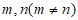 ,使得
,使得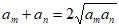 ;
;
③记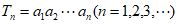 ,则数列
,则数列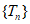 有最小项,其中所有正确结论的序号是
有最小项,其中所有正确结论的序号是
A. ① B. ③ C. ①③ D. ①②③
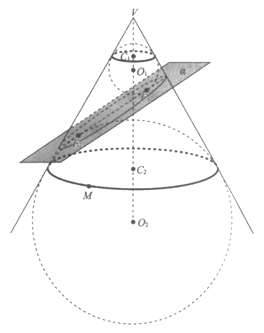
10. 如图所示,在圆锥内放入两个球O1,O2,它们都与圆锥相切(即与圆锥的每条母线相切),切点圆(图中粗线所示)分别为⊙C1,⊙C2,这两个球都与平面α相切,切点分别为F1,F2,丹德林(G.Dandelin)利用这个模型证明了平面α与圆锥侧面的交线为椭圆,F1,F2为此椭圆的两个焦点,这两个球也称为Dandelin双球,若圆锥的母线与它的轴的夹角为30°,⊙C1,⊙C2的半径分别为1,4,点M为⊙C2上的一个定点,点P为椭圆上的一个动点,则从点P沿圆锥表面到达点M的路线长与线段PF1的长之和的最小值是
A. 6 B. 8 C. 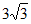 D.
D.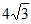
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
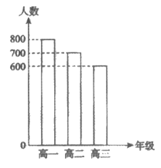
11. 在”互联网+”时代,国家积极推动信息化技术与传统教学方式的深度融合,实现线上、线下融合式教学模式变革。某校高一、高二和高三学生人数如图所示,采用分层抽样的方法调查融合式教学模式的实施情况,在抽取的样本中,高一学生有16人,则该样本中的高三学生人数为___________。
12. 设等比数列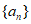 的前n项和为
的前n项和为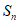 ,若
,若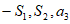 成等差数列,则数列
成等差数列,则数列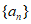 的公比为____________。
的公比为____________。
13. 已知双曲线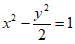 的左、右焦点分别为
的左、右焦点分别为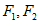 ,点
,点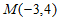 ,则该双曲线的渐近线方程为____________;
,则该双曲线的渐近线方程为____________;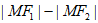 =__________。
=__________。
14. 已知函数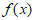 是定义域为R的奇函数,且
是定义域为R的奇函数,且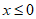 时,
时,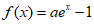 ,则a=________,
,则a=________,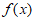 的值域是___________。
的值域是___________。
15. 已知圆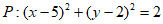 ,直线
,直线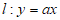 ,点
,点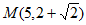 ,点
,点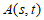 。
。
给出下列四个结论:
①当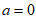 时,直线
时,直线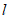 与圆P相离;
与圆P相离;
②若直线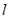 是圆P的一条对称轴,则
是圆P的一条对称轴,则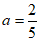 ;
;
③若直线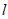 上存在点A,圆P上存在点N,使得∠MAN=90°,则a的最大值为
上存在点A,圆P上存在点N,使得∠MAN=90°,则a的最大值为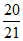 ;
;
④N为圆P上的一个动点,若∠MAN=90°,则t的最大值为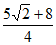 。
。
其中所有正确结论的序号是__________。
三、解答题:共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16. (本小题共15分)
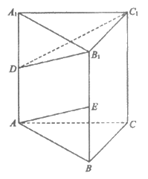
在三棱柱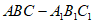 中,侧面
中,侧面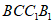 为矩形,AC⊥平面
为矩形,AC⊥平面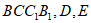 分别是棱
分别是棱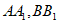 的中点。
的中点。
(Ⅰ)求证:AE∥平面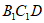 ;
;
(Ⅱ)求证:CC1⊥平面ABC;
(Ⅲ)若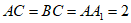 ,求直线AB与平面
,求直线AB与平面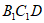 所成角的正弦值。
所成角的正弦值。
17.(本小题共14分)
若存在△ABC同时满足条件①、条件②、条件③、条件④中的三个,请选择一组这样的三个条件并解答下列问题:
(Ⅰ)求∠A的大小;
(Ⅱ)求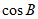 和a的值。
和a的值。
条件①: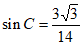 ;
;
条件②: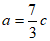 ;
;
条件③: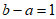 ;
;
条件④: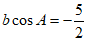 。
。
18.(本小题共14分)
某公司在2013~2021年生产经营某种产品的相关数据如下表所示:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
年生产台数(单位:万台) | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 10 | a |
年返修台数(单位:台) | 32 | 38 | 54 | 58 | 52 | 71 | 80 | 75 | b |
年利润(单位:百万台) | 3.85 | 4.50 | 4.20 | 5.50 | 6.10 | 9.65 | 10.00 | 11.50 | c |
注:年返修率=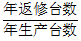 。
。
(Ⅰ)从2013~2020年中随机抽取一年,求该年生产的产品的平均利润不小于100元/台的概率;
(Ⅱ)公司规定:若年返修率不超过千分之一,则该公司生产部门当年考核优秀,现从2013~2020年中随机选出3年,记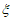 表示这3年中生产部门获得考核优秀的次数,求
表示这3年中生产部门获得考核优秀的次数,求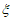 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)记公司在2013~2015年,2016~2018年,2019~2021年的年生产台数的方差分别为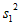 ,
,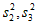 。若
。若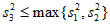 ,其中
,其中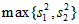 表示
表示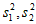 这两个数中最大的数,请写出a的最大值和最小值。(只需写出结论)
这两个数中最大的数,请写出a的最大值和最小值。(只需写出结论)
(注: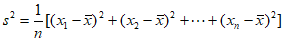 ,其中
,其中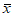 为数据
为数据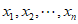 的平均数)
的平均数)
19. (本小题共14分)
已知椭圆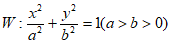 的离心率为
的离心率为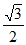 ,且经过点
,且经过点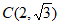 。
。
(Ⅰ)求椭圆W的方程及其长轴长;
(Ⅱ)A,B分别为椭圆W的左、右顶点,点D在椭圆W上,且位于x轴下方,直线CD交x轴于点Q。若△ACQ的面积比△BDQ的面积大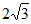 ,求点D的坐标。
,求点D的坐标。
20.(本小题共14分)
已知函数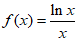 。
。
(Ⅰ)求函数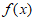 的单调区间;
的单调区间;
(Ⅱ)设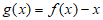 ,求证:
,求证: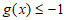 ;
;
(Ⅲ)设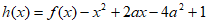 ,若存在
,若存在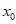 使得
使得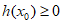 ,求a的最大值。
,求a的最大值。
21.(本小题共14分)
设A是由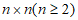 个实数组成的n行n列的数表,满足:每个数的绝对值是1,且所有数的和是非负数,则称数表A是”n阶非负数表”。
个实数组成的n行n列的数表,满足:每个数的绝对值是1,且所有数的和是非负数,则称数表A是”n阶非负数表”。
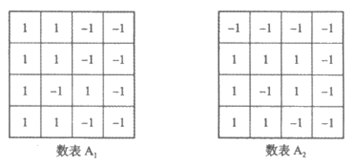
(Ⅰ)判断如下数表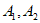 是否是”4阶非负数表”;
是否是”4阶非负数表”;
(Ⅱ)对于任意”5阶非负数表”A,记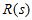 为A的第s行各数之和
为A的第s行各数之和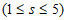 ,证明:存在
,证明:存在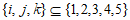 ,使得
,使得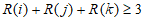 ;
;
(Ⅲ)当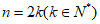 时,证明:对于任意”n阶非负数表”A,均存在k行k列,使得这k行k列交叉处的
时,证明:对于任意”n阶非负数表”A,均存在k行k列,使得这k行k列交叉处的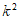 个数之和不小于k。
个数之和不小于k。
【试题答案】
一、选择题:共10小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | A | D | B | A | C | D | C | C | A |
二、填空题:共5小题,每小题5分,共25分。
题号 | 11 | 12 | 13 | 14 | 15 |
答案 | 12 | 3或-1 |
-2 | 1 (-1,1) | ①②④ |
三、解答题:共6小题,共85分。
16.(本小题共15分)
解:(Ⅰ)在三棱柱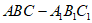 中,
中,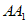 ∥
∥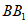 ,且
,且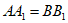 ,
,
因为点D,E分别是棱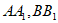 的中点,
的中点,
所以AD∥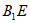 ,且
,且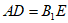 ,
,
所以四边形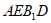 是平行四边形,
是平行四边形,
所以AE∥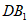 。
。
又因为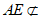 平面
平面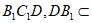 平面
平面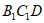 ,
,
所以AE∥平面 。
。
(Ⅱ)因为AC⊥平面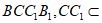 平面
平面 ,
,
所以AC⊥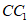 ,
,
因为侧面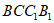 为矩形,
为矩形,
所以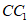 ⊥BC,
⊥BC,
又因为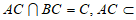 平面ABC,
平面ABC,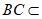 平面ABC,
平面ABC,
所以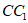 ⊥平面ABC。
⊥平面ABC。
(Ⅲ)分别以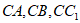 所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系
所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系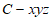 ,由题意得
,由题意得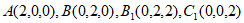 ,
,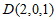 。
。
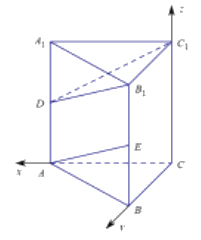
所以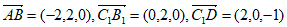 。
。
设平面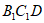 的法向量为
的法向量为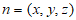 ,则
,则
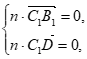 即
即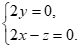
令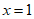 ,则
,则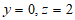 ,
,
于是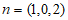 ,
,
所以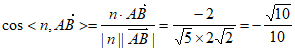 ,
,
所以,直线AB与平面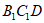 所成角的正弦值为
所成角的正弦值为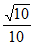 。
。
17.(本小题共14分)
选择①②③
解:(Ⅰ)因为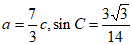 ,
,
由正弦定理得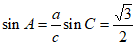 ,
,
因为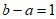 ,
,
所以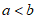 ,
,
所以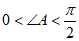 ,
,
所以∠A=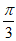 。
。
(Ⅱ)在△ABC中,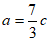 ,
,
所以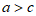 ,
,
所以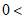 ∠C
∠C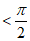 ,
,
因为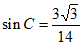 ,
,
所以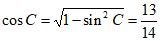 ,
,
所以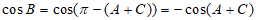
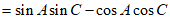
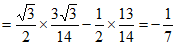 ,
,
所以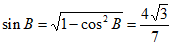 。
。
由正弦定理得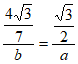 ,即
,即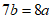 。
。
因为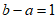 ,
,
所以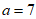 。
。
选择①②④
解:(Ⅰ)因为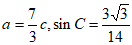 ,
,
由正弦定理得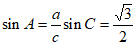 ,
,
在△ABC中,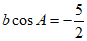 ,
,
所以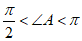 ,
,
所以∠A=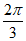 。
。
(Ⅱ)在△ABC中,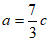 ,
,
所以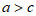 ,
,
所以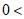 ∠C
∠C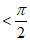 ,
,
因为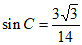 ,
,
所以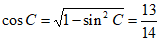 ,
,
所以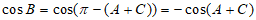
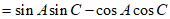
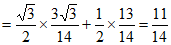 ,
,
所以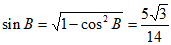 。
。
因为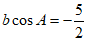 ,
,
所以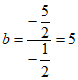 。
。
由正弦定理得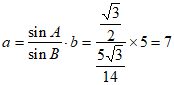 。
。
18.(本小题共14分)
解:(Ⅰ)由图表知,2013~2020年中,产品的平均利润小于100元/台的年份只有2015年,2016年,
所以从2013~2020年中随机抽取一年,该年生产的产品的平均利润不小于100元/台的概率为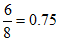 。
。
(Ⅱ)由图表知,2013~2020年中,返修率超过千分之一的年份只有2013,2015年,所以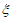 的所有可能取值为1,2,3,
的所有可能取值为1,2,3,
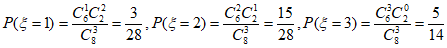 ,
,
所以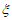 的分布列为
的分布列为
| 1 | 2 | 3 |
P |
|
|
|
故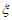 的数学期望
的数学期望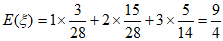 。
。
(Ⅲ)a的最大值为13,最小值为7。
19.(本小题共14分)
解:(Ⅰ)因为椭圆W经过点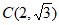 ,
,
所以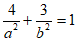 ,
,
因为椭圆W的离心率为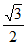 ,
,
所以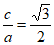 ,其中
,其中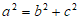 ,
,
所以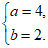
所以,椭圆W的方程为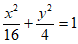 ,长轴长
,长轴长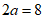 。
。
(Ⅱ)当直线CD的斜率不存在时,由题意可知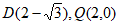 ,
,
由(Ⅰ)可知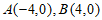 ,
,
所以△ACQ的面积为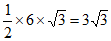 ,△BDQ的面积为
,△BDQ的面积为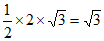 ,
,
显然△ACQ的面积比△BDQ的面积大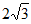 。
。
当直线CD的斜率存在时,由题意可设直线CD的方程为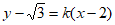 ,
,
且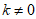 ,
,
令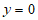 ,得
,得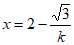 ,所以
,所以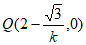 ,
,
由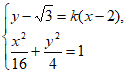 得
得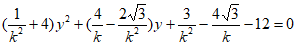 。
。
依题意可得点D的纵坐标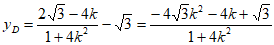 ,
,
因为点D在x轴下方,所以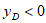 ,即
,即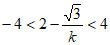 ,
,
所以△ACQ的面积为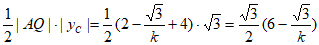 ,
,
△BDQ的面积为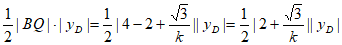
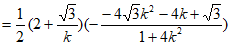
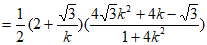 。
。
因为△ACQ的面积比△BDQ的面积大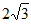 ,
,
所以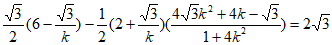 。
。
此方程无解。
综上所述,点D的坐标为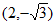 。
。
方法二
因为点D在x轴下方,所以点Q在线段AB(不包括端点)上,
由(Ⅰ)可知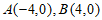 ,
,
所以△AOC的面积为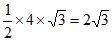 。
。
因为△ACQ的面积比△BDQ的面积大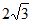 ,
,
所以点Q在线段OB(不包括端点)上,且△OCQ的面积等于△BDQ的面积,
所以△OCB的面积等于△BCD的面积,
所以OD∥BC。
设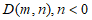 ,
,
则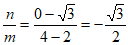 ,
,
因为点D在椭圆W上,
所以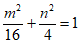 ,
,
所以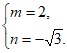
所以点D的坐标为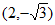 。
。
20.(本小题共14分)
解:(Ⅰ)因为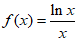 ,
,
所以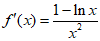 ,
,
令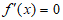 ,得
,得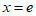 ,
,
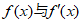 在区间
在区间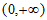 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| ↗ | 极大 | ↘ |
所以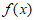 的单调递增区间为
的单调递增区间为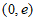 ,单调递减区间为
,单调递减区间为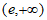 。
。
(Ⅱ)因为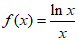 ,所以
,所以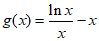 ,
,
所以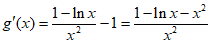 ,
,
①当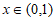 时,
时,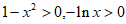 ,所以
,所以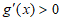 ;
;
②当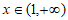 时,
时,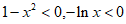 ,所以
,所以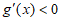 。
。
所以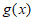 在
在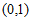 内单调递增,在
内单调递增,在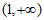 内单调递减,
内单调递减,
所以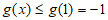 。
。
(Ⅲ)因为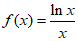 ,所以
,所以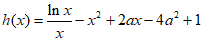 ,
,
①当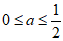 时,
时,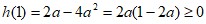 ,即存在1,使得
,即存在1,使得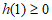 ;
;
②当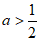 时,由(Ⅱ)可知,
时,由(Ⅱ)可知,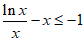 ,即
,即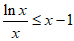 ,
,
所以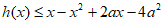
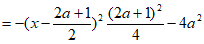
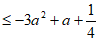
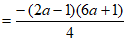
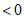 。
。
所以,对任意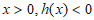 ,即不存在
,即不存在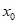 使得
使得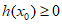 ,
,
综上所述,a的最大值为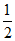 。
。
21.(本小题共14分)
解:记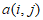 为数表A中第i行第j列的数,
为数表A中第i行第j列的数,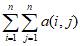
为数表A中所有数的和,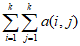 为数表A中前k行k列交叉处各数之和。
为数表A中前k行k列交叉处各数之和。
(Ⅰ)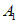 是”4阶非负数表”;
是”4阶非负数表”;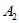 不是”4阶非负数表”。
不是”4阶非负数表”。
(Ⅱ)由题意知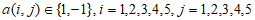 ,且数表A是”5阶非负数表”,
,且数表A是”5阶非负数表”,
所以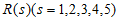 为奇数,且
为奇数,且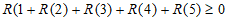 ,
,
不妨设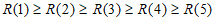 ,
,
①当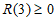 时,因为
时,因为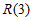 为奇数,所以
为奇数,所以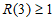 ,
,
所以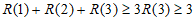 。
。
②当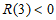 时,因为
时,因为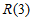 为奇数,所以
为奇数,所以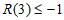 ,
,
所以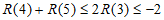 ,
,
所以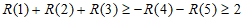 。
。
又因为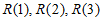 均为奇数,
均为奇数,
所以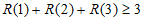 。
。
(Ⅲ)(1)先证明数表A中存在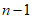 行n列
行n列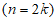 ,其所有数的和大于等于0,
,其所有数的和大于等于0,
设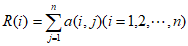 ,由题意知
,由题意知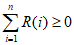 ,
,
不妨设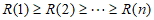 ,
,
由于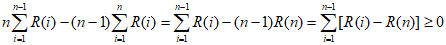 ,
,
所以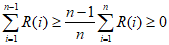 。
。
(2)由(1)及题意不妨设数表A前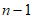 行n列
行n列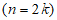 ,其所有数的和大于等于0。
,其所有数的和大于等于0。
下面考虑前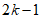 行,证明存在
行,证明存在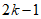 行k列,其所有数的和大于等于k,
行k列,其所有数的和大于等于k,
设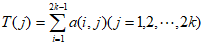 ,则
,则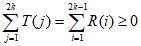 ,
,
不妨设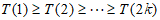 ,
,
因为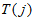 为
为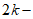 1个奇数的和,所以
1个奇数的和,所以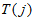 为奇数
为奇数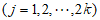 。
。
①当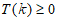 时,因为
时,因为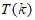 为奇数,所以
为奇数,所以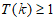 ,
,
所以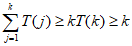 。
。
②当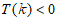 时,因为
时,因为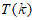 为奇数,所以
为奇数,所以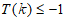 ,
,
所以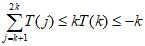 ,
,
所以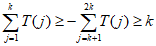 。
。
(3)在(2)所设数表A下,证明前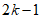 行前k列中存在k行k列,其所有数的和
行前k列中存在k行k列,其所有数的和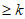 ,
,
设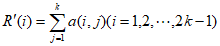 ,则
,则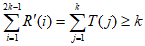 ,
,
不妨设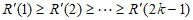 。
。
①当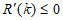 时,
时,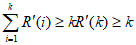 ;
;
②当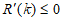 时,
时,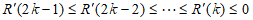 ,
,
所以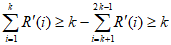 ,所以
,所以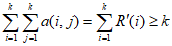 。
。
综上所述,对于任何”n阶非负数表”A,均存在k行k列,使得这k行k列交叉处的所有数之和不小于k。