(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合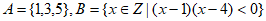 ,则
,则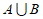 =
=
A. 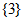 B.
B. 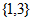 C.
C. 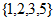 D.
D.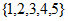
2. 下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是
A. 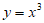 B.
B. 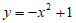 C.
C. 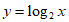 D.
D.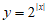
3. 在等比数列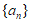 中,
中,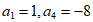 ,则
,则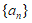 的前6项和为
的前6项和为
A. -21 B. 11 C. 31 D. 63
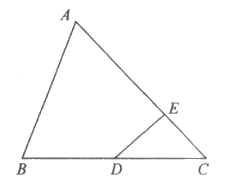
4. 如图,在△ABC中,点D,E满足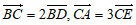 ,若
,若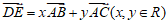 ,则
,则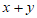 =
=
A. 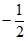 B.
B. 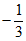 C.
C. 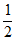 D.
D.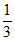
5. 已知抛物线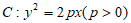 的焦点为F,准线为
的焦点为F,准线为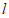 ,点A是抛物线C上一点,
,点A是抛物线C上一点,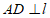 于D。若AF=4,∠DAF=60°,则抛物线C的方程为
于D。若AF=4,∠DAF=60°,则抛物线C的方程为
A. 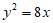 B.
B. 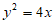 C.
C. 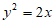 D.
D.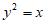
6. 现有甲、乙、丙、丁、戊5种在线教学软件,若某学校要从中随机选取3种作为教师”停课不停学”的教学工具,则其中甲、乙、丙至多有2种被选取的概率为
A. 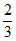 B.
B. 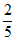 C.
C. 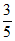 D.
D.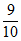
7. 在△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线经过点C,则该双曲线的离心率为
A. 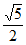 B.
B.  C.
C. 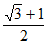 D.
D.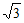
8. 已知函数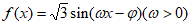 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为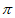 ,则”
,则”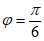 “是”
“是”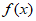 的图象关于直线
的图象关于直线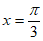 对称”的
对称”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 已知函数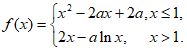 若关于x的不等式
若关于x的不等式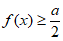 在R上恒成立,则实数a的取值范围为
在R上恒成立,则实数a的取值范围为
A. 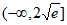 B.
B. 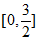 C.
C. 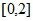 D.
D.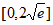
10. 如图,在正方体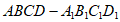 中,M,N分别是棱
中,M,N分别是棱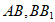 的中点,点P在对角线
的中点,点P在对角线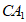 上运动。当△PMN的面积取得最小值时,点P的位置是
上运动。当△PMN的面积取得最小值时,点P的位置是
A. 线段 的三等分点,且靠近点A1
的三等分点,且靠近点A1
B. 线段 的中点
的中点
C. 线段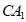 的三等分点,且靠近点C
的三等分点,且靠近点C
D. 线段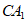 的四等分点,且靠近点C
的四等分点,且靠近点C
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
11. 若复数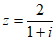 ,则
,则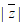 =__________。
=__________。
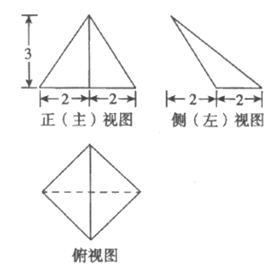
12. 已知某三棱锥的三视图如图所示,则该三棱锥的最长棱的长为____________,它的体积为____________。
13. 某购物网站开展一种商品的预约购买,规定每个手机号只能预约一次,预约后通过摇号的方式决定能否成功购买到该商品,规则如下:(i)摇号的初始中签率为0.19;(ii)当中签率不超过1时,可借助”好友助力”活动增加中签率,每邀请到一位好友参与”好友助力”活动可使中签率增加0.05,为了使中签率超过0.9,则至少需要邀请___________位好友参与到”好友助力”活动。
14. 已知函数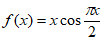 ,数列
,数列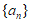 满足
满足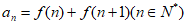 ,则数列
,则数列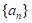 的前100项和是___________。
的前100项和是___________。
15. 数学中有许多寓意美好的曲线,曲线C: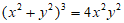 被称为”四叶玫瑰线”(如图所示)。
被称为”四叶玫瑰线”(如图所示)。
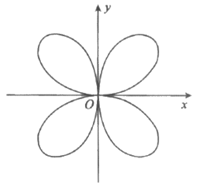
给出下列三个结论:
①曲线C关于直线y=x对称;
②曲线C上任意一点到原点的距离都不超过1:
③存在一个以原点为中心、边长为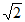 的正方形,使得曲线C在此正方形区域内(含边界)。
的正方形,使得曲线C在此正方形区域内(含边界)。
其中,正确结论的序号是___________。
注:本题给出的结论中,有多个符合题目要求,全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题14分)
在△ABC中,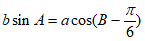 。
。
(Ⅰ)求B;
(Ⅱ)若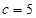 ,__________,求a。
,__________,求a。
从①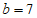 ,②
,②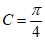 这两个条件中任选一个,补充在上面问题中并作答。
这两个条件中任选一个,补充在上面问题中并作答。
注:如果选择多个条件分别解答,按第一个解答计分。
17. (本小题14分)
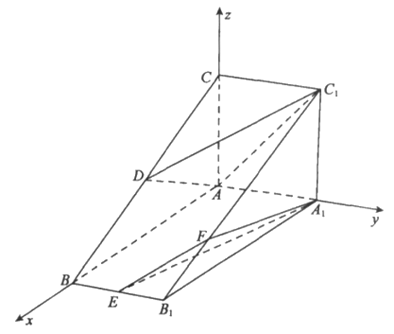
如图,在三棱柱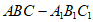 中,平面
中,平面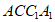 ⊥平面ABC,四边形
⊥平面ABC,四边形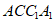 是正方形,点D,E分别是棱
是正方形,点D,E分别是棱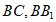 的中点,
的中点,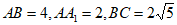 。
。
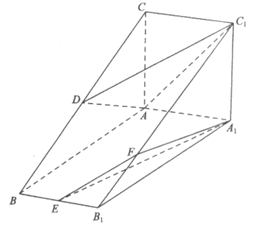
(Ⅰ)求证: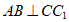 ;
;
(Ⅱ)求二面角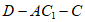 的余弦值;
的余弦值;
(Ⅲ)若点F在棱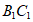 上,且
上,且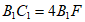 ,判断平面
,判断平面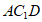 与平面
与平面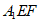 是否平行,并说明理由。
是否平行,并说明理由。
18. (本小题14分)
某科研团队研发了一款快速检测某种疾病的试剂盒,为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了80位患者和100位非患者,用该试剂盒分别对他们进行检测。结果如下:
患者的检测结果 | 人数 | 非患者的检测结果 | 人数 | |
阳性 | 76 | 阳性 | 1 | |
阴性 | 4 | 阴性 | 99 |
(Ⅰ)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(Ⅱ)从该地区患者中随机选取3人,各检测一次,假设每位患者的检测结果相互独立,以X表示检测结果为阳性的患者人数,利用(Ⅰ)中所得概率,求X的分布列和数学期望;
(Ⅲ)假设该地区有10万人,患病率为0.01,从该地区随机选取一人,用该试剂盒对其检测一次,若检测结果为阳性,能否判断此人患该疾病的概率超过0.5?并说明理由。
19.(本小题14分)
已知椭圆C: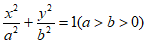 ,圆O:
,圆O: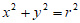 (O为坐标原点),过点
(O为坐标原点),过点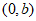 且斜率为1的直线与圆O交于点(1,2),与椭圆C的另一个交点的横坐标为
且斜率为1的直线与圆O交于点(1,2),与椭圆C的另一个交点的横坐标为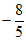 。
。
(Ⅰ)求椭圆C的方程和圆O的方程;
(Ⅱ)过圆O上的动点P作两条互相垂直的直线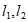 ,若直线
,若直线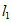 的斜率为
的斜率为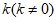 且
且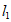 与椭圆C相切,试判断直线
与椭圆C相切,试判断直线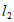 与椭圆C的位置关系,并说明理由。
与椭圆C的位置关系,并说明理由。
20.(本小题15分)
已知函数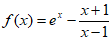 。
。
(Ⅰ)求曲线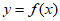 在点
在点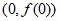 处的切线方程;
处的切线方程;
(Ⅱ)判断函数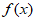 的零点的个数,并说明理由;
的零点的个数,并说明理由;
(Ⅲ)设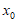 是
是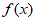 的一个零点,证明曲线
的一个零点,证明曲线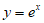 在点(
在点(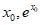 )处的切线也是曲线
)处的切线也是曲线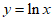 的切线。
的切线。
21.(本小题14分)
设数列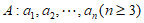 的各项均为正整数,且
的各项均为正整数,且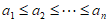 ,若对任意
,若对任意 ,存在正整数
,存在正整数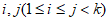 使得
使得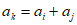 ,则称数列A具有性质T。
,则称数列A具有性质T。
(Ⅰ)判断数列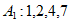 与数列
与数列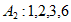 是否具有性质T;(只需写出结论)
是否具有性质T;(只需写出结论)
(Ⅱ)若数列A具有性质T,且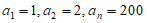 ,求n的最小值;
,求n的最小值;
(Ⅲ)若集合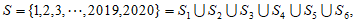 且
且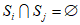 (任意
(任意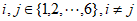 ),求证:存在
),求证:存在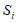 ,使得从
,使得从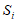 中可以选取若干元素(可重复选取)组成一个具有性质T的数列。
中可以选取若干元素(可重复选取)组成一个具有性质T的数列。
【试题答案】
第一部分(选择题 共40分)
一、选择题(共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项)
1. C 2. D 3. A 4. B 5. B
6. D 7. C 8. A 9. C 10. B
第二部分(非选择题 共110分)
二、填空题(共5小题,每小题5分,共25分)
11. 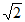 12. 5;4 13. 15 14. 100 15. ①②
12. 5;4 13. 15 14. 100 15. ①②
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
16.(本小题14分)
解:(Ⅰ)因为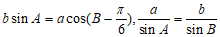 ,所以
,所以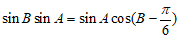 ,
,
又因为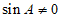 ,所以
,所以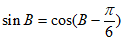 ,即
,即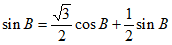 ,
,
所以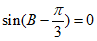 。
。
又因为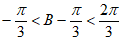 ,所以
,所以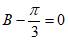 ,所以
,所以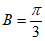 。
。
(Ⅱ)若选①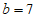 ,则在△ABC中,由余弦定理
,则在△ABC中,由余弦定理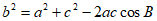 ,
,
得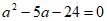 ,解得
,解得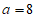 或
或 (舍),所以
(舍),所以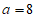 。
。
若选②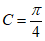 ,则
,则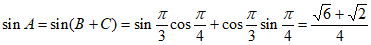 ,
,
由正弦定理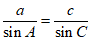 ,
,
得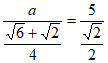 ,解得
,解得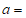
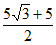 。
。
所以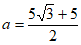 。 14分
。 14分
17.(本小题14分)
解:(Ⅰ)因为四边形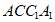 是正方形,
是正方形,
所以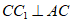 。
。
又因为平面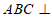 平面
平面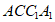 ,
,
平面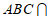 平面
平面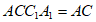 ,
,
所以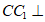 平面ABC,
平面ABC,
又因为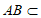 平面ABC,
平面ABC,
所以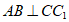 。
。
(Ⅱ)由(Ⅰ)知,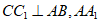 ∥
∥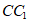 ,
,
所以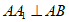 。
。
又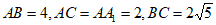 ,
,
所以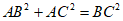 ,
,
所以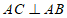 。
。
如图,以A为原点,建立空间直角坐标系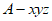 ,
,
所以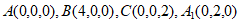 ,
,
则有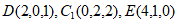 ,
,
平面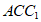 的一个法向量为
的一个法向量为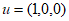 ,
,
设平面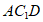 的一个法向量为
的一个法向量为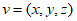 ,
,
又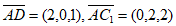 ,
,
由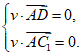 得
得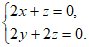
令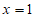 ,则
,则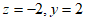 ,所以
,所以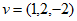 。
。
设二面角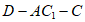 的平面角为
的平面角为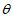 ,则
,则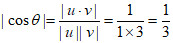 。
。
由题知,二面角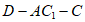 为锐角,所以其余弦值为
为锐角,所以其余弦值为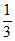 。
。
(Ⅱ)平面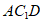 与平面
与平面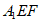 不平行,理由如下:
不平行,理由如下:
由(Ⅱ)知,平面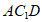 的一个法向量为
的一个法向量为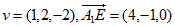 ,
,
所以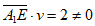 ,所以
,所以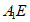 与平面
与平面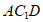 不平行。
不平行。
又因为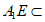 平面
平面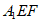 ,
,
所以平面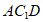 与平面
与平面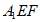 不平行。 14分
不平行。 14分
18.(本小题14分)
(Ⅰ)由题意知,80位患者中有76位用该试剂盒检测一次,结果为阳性。
所以从该地区患者中随机选取一位,用该试剂盒检测一次,结果为阳性的概率估计为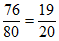 。
。
(Ⅱ)由题意可知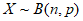 ,其中
,其中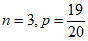 。
。
X的所有可能的取值为0,1,2,3。
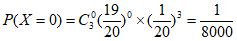 ,
,
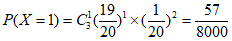 ,
,
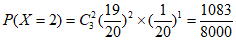 ,
,
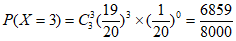 。
。
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故X的数学期望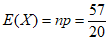 。
。
(Ⅲ)此人患该疾病的概率未超过0.5,理由如下:
由题意得,如果该地区所有人用该试剂盒检测一次,那么结果为阳性的人数为
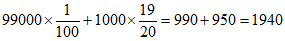 ,其中患者人数为950。
,其中患者人数为950。
若某人检测结果为阳性,那么他患该疾病的概率为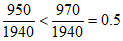 ,
,
所以此人患该疾病的概率未超过0.5。 14分
19.(本小题14分)
解:(Ⅰ)因为圆O过点(1,2),所以圆O的方程为: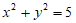 ,
,
因为过点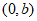 且斜率为1的直线方程为
且斜率为1的直线方程为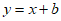 ,
,
又因为过点(1,2),所以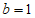 ,
,
因为直线与椭圆相交的另一个交点坐标为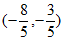 ,
,
所以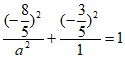 ,解得
,解得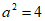 ,
,
所以椭圆C的方程为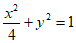 。
。
(Ⅱ)直线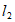 与椭圆C相切,理由如下:
与椭圆C相切,理由如下:
设圆O上动点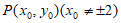 ,所以
,所以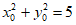 。
。
依题意,设直线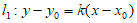 。
。
由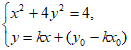 得
得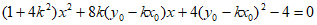 。
。
因为直线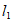 与椭圆C相切,
与椭圆C相切,
所以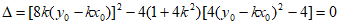 ,
,
所以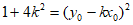 ,所以
,所以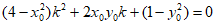 。
。
因为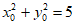 ,所以
,所以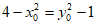 ,
,
所以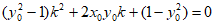 。
。
设直线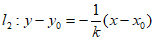 ,
,
由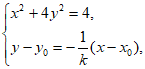
得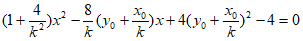 ,
,
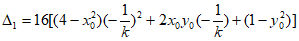
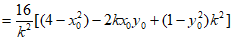
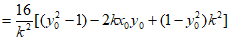
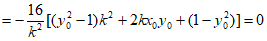 ,
,
所以直线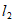 与椭圆C相切。 14分
与椭圆C相切。 14分
20.(本小题15分)
解:(Ⅰ)因为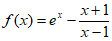 ,
,
所以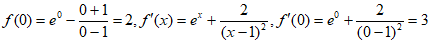 ,
,
所以曲线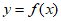 在点
在点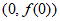 处的切线的方程为
处的切线的方程为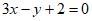 。
。
(Ⅱ)函数f(x)有且仅有两个零点,理由如下:
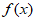 的定义域为
的定义域为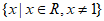 。
。
因为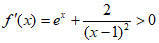 ,
,
所以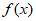 在
在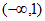 和
和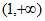 上均单调递增。
上均单调递增。
因为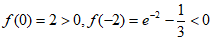 ,
,
所以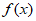 在
在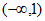 上有唯一零点
上有唯一零点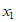 。
。
因为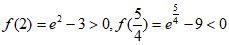 ,
,
所以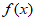 在
在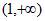 上有唯一零点
上有唯一零点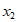 ,
,
综上,f(x)有且仅有两个零点。
(Ⅲ)曲线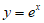 在点
在点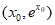 处的切线方程为
处的切线方程为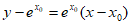 ,
,
即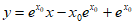 ,
,
设曲线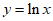 在点
在点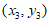 处的切线斜率为
处的切线斜率为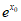 ,
,
则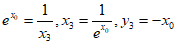 ,即切点为
,即切点为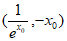 ,
,
所以曲线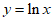 在点
在点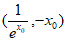 处的切线方程为
处的切线方程为
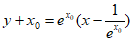 ,即
,即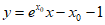 。
。
因为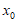 是
是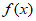 的一个零点,所以
的一个零点,所以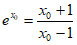 ,
,
所以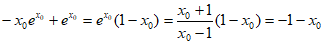 ,
,
所以这两条切线重合,
所以结论成立。 15分
21.(本小题14分)
解:(Ⅰ)数列A1不具有性质T;数列A2具有性质T。
(Ⅱ)由题可知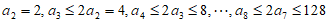 ,
,
所以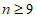 。
。
若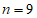 ,因为
,因为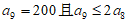 ,所以
,所以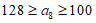 。
。
同理,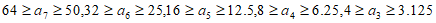 ,
,
因为数列各项均为正整数,所以a3=4,所以数列前三项为1,2,4。
因为数列A具有性质T,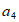 只可能为4,5,6,8之一,而又因为
只可能为4,5,6,8之一,而又因为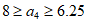 ,
,
所以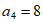 ,
,
同理,有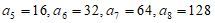 ,
,
此时数列为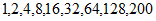 ,
,
但数列中不存在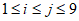 使得
使得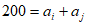 ,所以该数列不具有性质T,
,所以该数列不具有性质T,
所以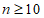 。
。
当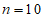 时,取
时,取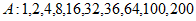 。(构造数列不唯一)
。(构造数列不唯一)
经验证,此数列具有性质T,
所以,n的最小值为10。
(Ⅲ)反证法:假设结论不成立,即对任意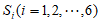 都有:
都有:
若正整数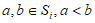 ,则
,则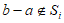 ,
,
否则,当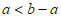 时,
时,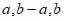 是一个具有性质T的数列;
是一个具有性质T的数列;
当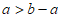 时,
时,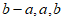 是一个具有性质T的数列;
是一个具有性质T的数列;
当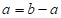 时,
时,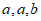 是一个具有性质T的数列。
是一个具有性质T的数列。
(i)由题意可知,这6个集合中至少有一个集合的元素个数不少于337个,不妨设此集合为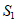 ,从
,从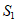 中取出337个数,记为
中取出337个数,记为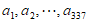 ,且
,且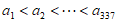 。
。
令集合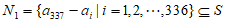 ,
,
由假设,对任意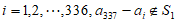 ,所以
,所以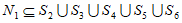 。
。
(ii)在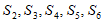 中至少有一个集合包含
中至少有一个集合包含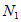 中的至少68个元素,不妨设这个集合为
中的至少68个元素,不妨设这个集合为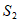 ,从
,从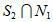 中取出68个数,记为
中取出68个数,记为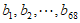 ,且
,且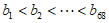 。
。
令集合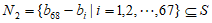 ,
,
由假设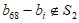 ,
,
对任意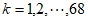 ,存在
,存在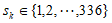 使得
使得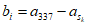 ,
,
所以对任意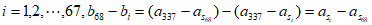 ,
,
由假设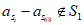 ,所以
,所以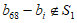 ,所以
,所以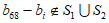 ,
,
所以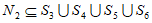 。
。
(iii)在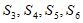 中至少有一个集合包含
中至少有一个集合包含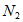 中的至少17个元素,不妨设这个集合为
中的至少17个元素,不妨设这个集合为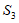 ,从
,从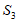
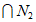 中取出17个数,记为
中取出17个数,记为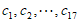 ,且
,且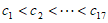 ,
,
令集合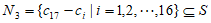 ,
,
由假设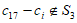 。
。
对任意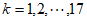 ,存在
,存在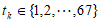 使得
使得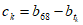 ,
,
所以对任意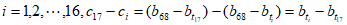 ,
,
同样,由假设可得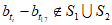 ,所以
,所以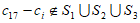 ,
,
所以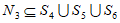 。
。
(iv)类似地,在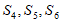 中至少有一个集合包含
中至少有一个集合包含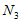 中的至少6个元素,
中的至少6个元素,
不妨设这个集合为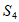 ,从
,从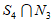 中取出6个数,记为
中取出6个数,记为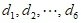 ,
,
且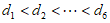 ,则
,则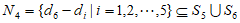 。
。
(v)同样,在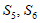 中至少有一个集合包含
中至少有一个集合包含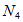 中的至少3个元素,
中的至少3个元素,
不妨设这个集合为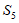 ,从
,从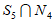 中取出3个数,记为
中取出3个数,记为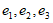 ,且
,且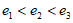 ,
,
同理可得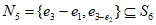 。
。
(vi)由假设可得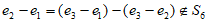 ,
,
同上可知,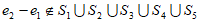 ,
,
而又因为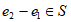 ,所以
,所以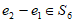 ,矛盾,
,矛盾,
所以假设不成立,
所以原命题得证。 14分