本试卷有三道大题,考试时长120分钟,满分150分。
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设集合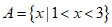 ,集合
,集合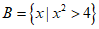 ,则集合A
,则集合A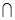 B等于( ).
B等于( ).
(A){x|2<x<3} (B){x|x >1}
(C){x|1<x<2} (D){x|x>2}
2. 已知命题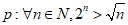 ,则
,则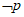 是( )
是( )
(A)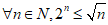 (B)
(B)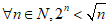
(C)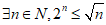 (D)
(D)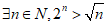
3. 已知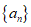 是公差为d的等差数列,Sn为其前n项和. 若S3=3a1+3,则d=( )
是公差为d的等差数列,Sn为其前n项和. 若S3=3a1+3,则d=( )
(A) -2 (B) -1 (C)1 (D)2
4. 若函数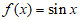 ,则
,则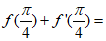 ( )
( )
(A)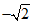 (B)
(B) 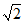 (C)1 (D)0
(C)1 (D)0
5. 若抛物线y2=4x上的点A到焦点的距离为10,则点A到y轴的距离是( )
(A)6 (B)7 (C)8 (D)9
6. 等差数列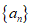 的首项为1,公差不为0,若a1,a2,a4成等比数列,则
的首项为1,公差不为0,若a1,a2,a4成等比数列,则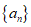 前5项的和为( )
前5项的和为( )
(A)10 (B) 15 (C)21 (D) 28
7. 已知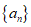 是等比数列,Sn为其前n项和,那么“a1>0″是“数列{Sn}为递增数列“的 ( )
是等比数列,Sn为其前n项和,那么“a1>0″是“数列{Sn}为递增数列“的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
8. 已知函数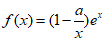 ,若
,若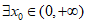 ,x0为f(x)的一个极大值点,则实数a的取值范围是( )
,x0为f(x)的一个极大值点,则实数a的取值范围是( )
(A)(-∞,0) (B)(4,+∞)
(C)(-∞,0)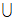 (4,+∞) (D)前三个答案都不对
(4,+∞) (D)前三个答案都不对
9. 已知正方体ABCD-A1B1C1D1,空间中与三条棱AB,CC1,A1D1所在的直线距离相等的点( )
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
10. 定义在区间[a,b]上的连续函数y=f(x),如果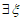 ∈[a,b],使得
∈[a,b],使得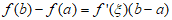 ,则称
,则称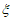 为区间[a,b]上的“中值点“. 下列函数:
为区间[a,b]上的“中值点“. 下列函数:
①f(x)=3x+2;
②f(x)=x2-x+1;
③f(x)=ln(x+1);
④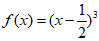 中,在区间[0,1]上“中值点“多于一个的函数序号为( )
中,在区间[0,1]上“中值点“多于一个的函数序号为( )
(A) ①② (B)①③ (C)②③ (D)①④
二、填空题共6小题,每小题5分,共30分。
11. 若复数z满足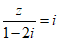 ,其中i为虚数为单位,则|z|=_____________.
,其中i为虚数为单位,则|z|=_____________.
12. 若3名演讲比赛获奖学生和2名指导教师站在一排照相,则2名指导教师不相邻的站法有_______种. (用数字作答)
13. 已知x>0,y>0,xy=1,则x+4y的最小值为_________,此时x的值为_________.
14. 设函数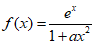 ,其中a>0.若对于任意x∈R,f'(x)≥0,则实数a的取值范围是_________.
,其中a>0.若对于任意x∈R,f'(x)≥0,则实数a的取值范围是_________.
15. 设函数y=f(x)的定义域为D,若对任意x1∈D,存在x2∈D,使得f(x1)·f(x2) =1,则称函数f(x)具有性质M,给出下列四个结论:
①函数y=x3-x不具有性质M;
②函数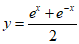 具有性质M;
具有性质M;
③若函数y=log8(x+2),x∈[0,t]具有性质M,则t=510;
④若函数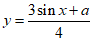 具有性质M,则a=5.
具有性质M,则a=5.
其中,正确结论的序号是_____________.
三、解答题共6小题,共80分。解答应写出文字说明、演算步骤或证明过程。
16. 已知等差数列{an}的前n项和为Sn,且a2=5,S3=a7.
(I)求数列{an}的通项公式;
(II)若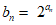 ,求数列{an+bn}的前n项和.
,求数列{an+bn}的前n项和.
17. 已知函数f(x)=x3-3x+1.
(I)求函数f(x)的极值;
(II)求函数f(x)在[0,2]上的最大值;
18. 已知函数f(x)=x+alnx(a∈R).
(I)当a=-1时,求函数f(x)的极值;
(Ⅱ)若不等式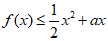 对任意x>0恒成立,求a的取值范围.
对任意x>0恒成立,求a的取值范围.
19. 已知椭圆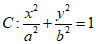
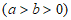 过点
过点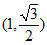 ,且C的离心率为
,且C的离心率为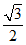 .
.
(I)求椭圆C的方程;
(II)过点P(1,0)的直线l交椭圆C于A,B两点,求|PA|·|PB|的取值范围.
20. 已知函数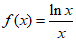 .
.
(I)求函数在点(1,0)处的切线方程;
(Ⅱ)设实数k使得不等式f(x)<kx恒成立,求k的范围;
(Ⅲ)设函数h(x)=f(x)-kx(k∈R),求函数h(x)在区间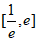 上的零点个数.
上的零点个数.
21. 数列An:a1,a2,…,an(n≥4)
满足:a1=1,an=m,ak+1 -ak=0或1(k=1,2,…,n-1).
对任意i,j,都存在s,t,使得ai+aj=as+at,其中i,j,s,t∈{1,2,…,n)且两两不相等.
(I)若m=2,写出下列三个数列中所有符合题目条件的数列的序号:
①1,1,1,2,2,2; ②1,1,1,1,2,2,2,2; ③1,1,1,1,1,2,2,2,2
( II)记S=a1+a2+…+an. 若m=3,求S的最小值;
(Ⅲ)若m=2018,求n的最小值.
参考答案
一、选择题共10小题,每小题4分,共40分。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A | C | C | B | D | B | B | B | D | D |
二、填空题共5小题,每小题5分,共25分。
11. 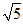 ; 12. 72; 13. 4;2; 14. (0,1]; 15. ①③;
; 12. 72; 13. 4;2; 14. (0,1]; 15. ①③;
三、解答题共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16. 解:(I)设等差数列{an}的首项为a1,公差为d.
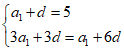
解得a1=3, d=2
由an=a1+(n-1)d,则an=2n+1
因此,通项公式为an=2n+1.
(II)由(I)可知:an=2n+1,则bn=22n+1
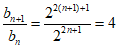
因为b1=23=8,
所以{bn}是首项为8,公比为q=4的等比数列.
记{an+bn}的前n项和为Tn,则
Tn= (a1+b1)+(a2+b2)+…+(an+bn)
= (a1+a2+…+an)+(b1+b2+…+bn)
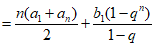
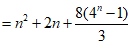
17. 解:(I)极大值f(-1) =3,极小值f(1)=-1;(II)最大值f(2)=3
18. 解:函数f(x)=x+alnx的定义域为(0,+∞),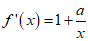 .
.
(I)当a=-1时,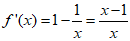
令f'(x)=0,得x=1.
当x变化时,f'(x),f (x)的变化情况如下:
x | (0,1) | 1 | (1,+∞) |
f'(x) | – | 0 | + |
f(x) | ↘ | 极小值f(1)=1 | ↗ |
所以f(x)的极小值为f(1)=1,无极大值.
(II)不等式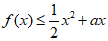 恒成立等价于
恒成立等价于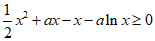 恒成立.
恒成立.
令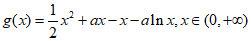 .
.
所以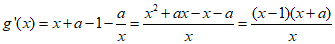
(1)当a≥0时,因为x∈(0,+∞),所以x+a>0.
令g'(x)=0,得x=1.
当x变化时,g'(x),g(x)的变化情况如下:
x | (0,1) | 1 | (1,+∞) |
g'(x) | – | 0 | + |
g(x) | ↘ | 最小值 | ↗ |
当a≥0时,不等式g(x)≥0恒成立当且仅当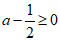 .
.
所以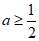 符合题意.
符合题意.
(2)当a=-1时,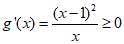 .
.
所以g(x)在(0,+∞)内单调递增.
因为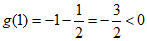 ,所以g(x)≥0不恒成立.
,所以g(x)≥0不恒成立.
所以a=-1不符合题意.
(3)当-1<a<0时,0<-a<1.
当x变化时,g'(x),g(x)的变化情况如下:
x | (0,-a) | -a | (-a,1) | 1 | (1,+∞) |
g’(x) | + | 0 | – | 0 | + |
g(x) | ↗ | 极大值g(-a) | ↘ | 极小值 | ↗ |
因为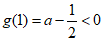 ,所以g(x)≥0不恒成立.
,所以g(x)≥0不恒成立.
所以-1<a<0不符合题意.
(4)当a<-1时,-a>1.
当x变化时,g'(x),g(x)的变化情况如下:
x | (0,1) | 1 | (1,-a) | -a | (-a,+∞) |
g'(x) | + | 0 | – | 0 | + |
g(x) | ↗ | 极大值 | ↘ | 极小值g(-a) | ↗ |
因为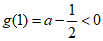 ,所以g(x)≥0不恒成立.
,所以g(x)≥0不恒成立.
所以a<-1不符合题意.
综上所述,a的取值范围是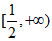 .
.
((2)(3)(4)可由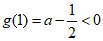 判断出不符合题意)
判断出不符合题意)
19. 解:(I)由题意得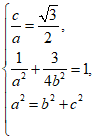 ,解得
,解得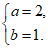
所以椭圆C的方程为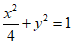 .
.
(II)当直线l的斜率不存在时,直线l:x=1与椭圆C交于A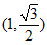 ,B
,B 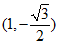 两点,
两点,
所以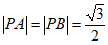 ,所以
,所以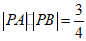 .
.
当直线l的斜率存在时,设其方程为y=k(x-1),
由
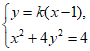
得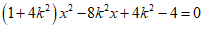 .
.
且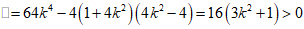 .
.
设A(x1,y1),B(x2,y2),则
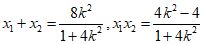 .
.
所以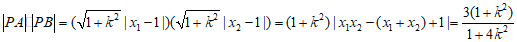 .
.
令t=1+4k2,则t≥1,
所以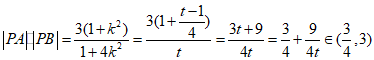 .
.
当t=1,即k=0时,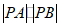 取最大值3.
取最大值3.
综上所述,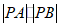 的取值范围是
的取值范围是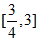 .
.
20. 解:(I) y=x-1;
(II)因为x>0,所以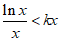 恒成立等价于
恒成立等价于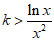 恒成立,
恒成立,
令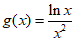 ,再求函数
,再求函数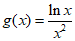 的最大值
的最大值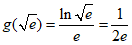 ,得k的范围是k>
,得k的范围是k>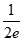 ;
;
(Ⅲ)由h(x)=f(x)-kx=0,得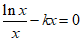 ,即lnx-kx2=0,
,即lnx-kx2=0, 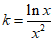 ,
,
研究函数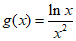 ,
,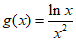 的最大值
的最大值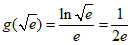 ,
,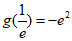 ,
,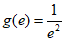
所以,当k>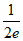 或者
或者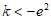 时,有0个零点;
时,有0个零点;
当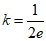 或者
或者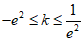 时,有1个零点;
时,有1个零点;
当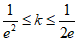 时,有2个零点;
时,有2个零点;
21. 解:(I)②③.
(II)当m=3时,设数列An中1,2,3出现频数依次为q1,q2,q3,由题意qi≥1(i=1,2,3).
①假设q1<4,则有a1+a2<as+at(对任意s>t>2),
与已知矛盾,所以q1≥4. 同理可证:q3≥4.
②假设q2=1,则存在唯一的k∈{1,2,…,n},使得ak=2.
那么,对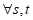 ,有a1+ak=1+2≠as+at (k,s,t两两不相等),与已知矛盾,所以q2≥2.
,有a1+ak=1+2≠as+at (k,s,t两两不相等),与已知矛盾,所以q2≥2.
综上:q1≥4,q3≥4,q2≥2,所以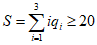 .
.
(Ⅲ)设1,2,…,2018出现频数依次为q1,q2,…,q2018.
同(II)的证明,可得q1≥4,q2018≥4,q2≥2,q2017≥2,则n≥2026.
取q1=q2018=4,q2=q2017=2,qi=1,i=3,4,5,…,2016,得到的数列为:
Bn:1,1,1,1,2,2,3,4,……, 2015,2016,2017, 2017, 2018,2018, 2018, 2018.
下面证明Bn满足题目要求. 对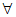 i,j∈{1,2,…,2026),不妨令ai≤aj,
i,j∈{1,2,…,2026),不妨令ai≤aj,
①如果ai=aj=1或ai=aj=2018,由于q1=4,q2018=4,所以符合条件;
②如果ai=1,aj=2或ai=2017,aj=2018,由于q1 =4,q2018=4,q2=2,q2017=2,所以也成立;
③如果ai=1,aj>2,则可选取as=2,at=aj-1;同样的,如果ai<2017,aj=2018,
则可选取as=ai+1,at=2017,使得ai+aj=as+at,且i,j,s,t两两不相等;
④如果1<ai≤aj<2018,则可选取as=ai-1,at=aj+1,注意到这种情况每个数最多被选取了一次,因此也成立.
综上,对任意i,j,总存在s,t,使得ai+aj=as+at,其中i,j,s,t∈{1,2,…,n}且两两不相等. 因此Bn满足题目要求,所以n的最小值为2026.