本试卷共三道大题,28道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
下面各题均有四个选项,符合题意的选项只有一个。
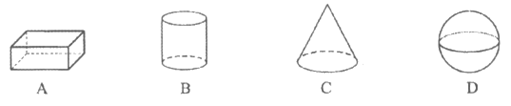
1. 下列几何体中,是长方体的为
2. 2020年11月10日,中国“奋斗者“号载人潜水器在马里亚纳海沟成功坐底,坐底深度10 909米,刷新中国载人深潜的新纪录,将10 909用科学记数法表示应为
A. 0.10909×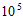 B. 1.0909×
B. 1.0909×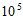 C. 1.0909×
C. 1.0909×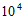 D. 10.909×
D. 10.909×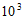
3. 实数m,n在数轴上的对应点的位置如图所示,则正确的结论是
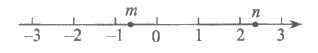
A. 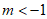 B.
B. 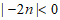 C.
C. 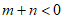 D.
D.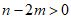
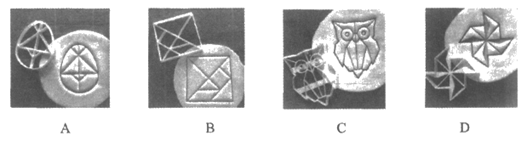
4. 在下列面点烘焙模具中,其图案是中心对称图形的是
5. 若一个多边形的内角和为540°,则这个多边形的边数是
A. 6 B. 5 C. 4 D. 3
6. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架. 其中《盈不足》卷记载了一道有趣的数学问题:”今有共买物,人出八,赢三;人出七,不足四,问人数、物价各几何?“译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数、物价各多少?“设人数为x人,物价为y钱,根据题意,下面所列方程组正确的是

A. 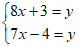 B.
B. 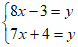 C.
C. 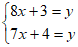 D.
D.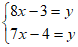
7. 下列两个变量之间的关系为反比例关系的是
A. 圆的周长与其半径的关系
B. 平行四边形面积一定时,其一边长与这边上的高的关系
C. 销售单价一定时,销售总价与销售数量的关系
D. 汽车匀速行驶过程中,行驶路程与行驶时间的关系
8. 如图为某二次函数的部分图象,有如下四个结论:
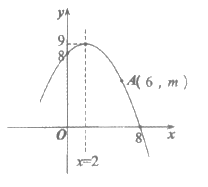
①此二次函数表达式为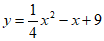
②若点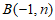 在这个二次函数图象上,则
在这个二次函数图象上,则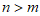
③该二次函数图象与x轴的另一个交点为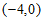
④当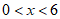 时,
时,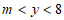
所有正确结论的序号是
A. ①③ B. ①④ C. ②③ D. ②④
二、填空题(本题共16分,每小题2分)
9. 若二次根式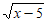 有意义,则x的取值范围是_______________。
有意义,则x的取值范围是_______________。
10. 分解因式: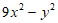 =_______________。
=_______________。
11. 若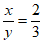 ,则代数式
,则代数式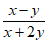 的值是_____________。
的值是_____________。
12. 不透明的盒子中有3个红球,1个白球,这些球除颜色外无其他差别,从中随机摸出一个球不放回,再从中随机摸出一个球,两次摸出的恰好都是红球的概率是____________。
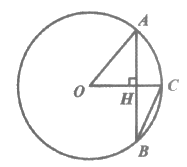
13. 如图,在⊙O中,半径OC⊥AB于点H,若∠OAB=40°,则∠ABC=___________°。
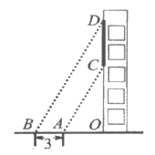
14. 如图,小石同学在A,B两点分别测得某建筑物上条幅两端C,D两点的仰角均为60°,若点O,A,B在同一直线上,A,B两点间距离为3米,则条幅的高CD为___________米(结果可以保留根号)。
15. 为了解某市常住人口的变化情况,收集并整理了2011年至2020年的常住人口(单位:万人)数据,绘制统计图如下:
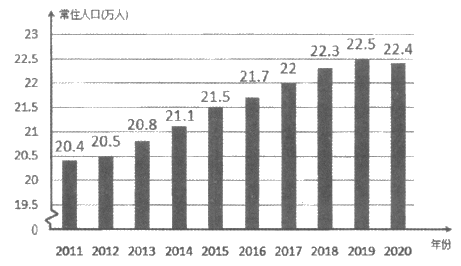
根据统计图,写出一条有关该市常住人口变化情况的信息:______________。
16. 某餐厅在客人用餐完毕后收拾餐桌分以下几个步骤:①回收餐具与剩菜、清洁桌面;②清洁椅面与地面;③摆放新餐具。前两个步骤顺序可以互换,但摆放新餐具必须在前两个步骤都完成之后才可进行,每个步骤所花费时间如下表所示:
桌别 | 回收餐具与剩菜、清洁桌面 | 清洁椅面与地面 | 摆放新餐具 |
大桌 | 5 | 3 | 2 |
小桌 | 3 | 2 | 1 |
现有三名餐厅工作人员分别负责①回收餐具与剩菜、清洁桌面,②清洁椅面与地面,③摆放新餐具,每张桌子同一时刻只允许一名工作人员进行工作,现有两张小桌和一张大桌需要清理,那么将三张桌子收拾完毕最短需要__________分钟。
三、解答题(本题共68分,第17—22题,每小题5分,第23—26题,每小题6分,第27—28题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 计算: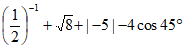 。
。
18. 解不等式组: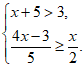
19. 下面是小景设计的“过直线外一点作这条直线的垂线“的尺规作图过程。
已知:如图1,直线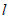 和
和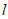 外一点A。
外一点A。
求作:直线AE,使得AE⊥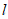 于点E。
于点E。
作法:①在直线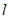 上取一点B,连接AB(如图2);
上取一点B,连接AB(如图2);
②作线段AB的垂直平分线CD,交AB于点O;
③以O为圆心,OB长为半径作圆,交直线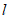 于点E;
于点E;
④作直线AE。
所以直线AE即为所求作的直线。
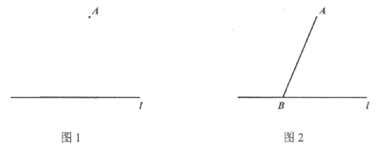
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明。
证明:∵CD为线段AB的垂直平分线,
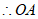 =___________。
=___________。
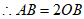 ,
,
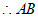 是⊙O的直径,
是⊙O的直径,
∴∠AEB=90°(________________________)(填推理的依据),
∴AE⊥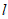 。
。
20. 关于x的一元二次方程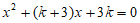 。
。
(1)求证:方程总有两个实数根;
(2)若该方程有一个根大于1,求k的取值范围。
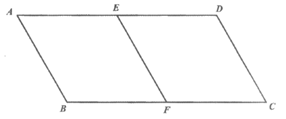
21. 如图,在平行四边形ABCD中,BC=2CD,E,F分别是AD,BC的中点,连接EF。
(1)求证:四边形EFCD是菱形;
(2)连接AF,若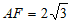 ,∠DEF=60°,则EF的长为__________;菱形EFCD的面积为____________。
,∠DEF=60°,则EF的长为__________;菱形EFCD的面积为____________。
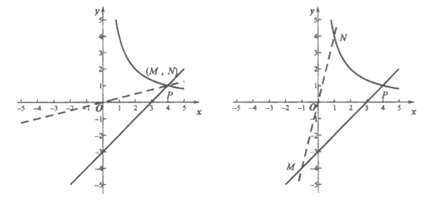
22. 在平面直角坐标系xOy中,直线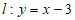 与函数
与函数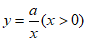 的图象G交于点
的图象G交于点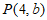 。
。
(1)求a,b的值;
(2)直线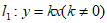 与直线
与直线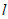 交于点M,与图象G交于点N,点M到y轴的距离记为
交于点M,与图象G交于点N,点M到y轴的距离记为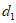 ,点N到y轴的距离记为
,点N到y轴的距离记为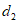 ,当
,当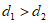 时,直接写出k的取值范围。
时,直接写出k的取值范围。
23. 如图,OA是⊙O的半径,AB与⊙O相切于点A,点C在⊙O上且AC=AB,为AC的中点,连接OD,连接CB交OD于点E,交OA于点F。
(1)求证:OE=OF;
(2)若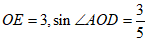 ,求BF的长。
,求BF的长。
24. 阅读下面材料:
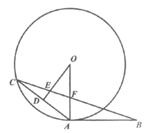
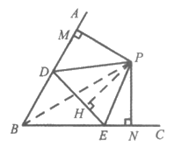
小石遇到这样一个问题:如图1,∠ABC=90°,D,E分别是∠ABC的边BA,BC上的动点(不与点B重合),∠ADE与∠DEC的角平分线交于点P,△DBE的周长为a,过点P作PM⊥BA于点M,PN⊥BC于点N,求PM+PN与△DBE的周长a的数量关系。
小石通过测量发现了垂线段PM与PN的数量关系,从而构造全等三角形和直角三角形,经过推理和计算使问题得到解决。
请回答:线段PM与PN的数量关系为____________;
PM+PN与a的数量关系是__________。
参考小石思考问题的方法,解决问题:
如图2,当∠ABC=60°时,其它条件不变,判断点P到DE的距离PH与△DBE的周长a的数量关系,并简要说明理由。
25. 某校举行“云端好声音“线上歌唱比赛活动丰富同学们的居家生活,由1至4号的专业评委和5至10号的大众评委进行评分。
例如 A节目演出后各个评委所给分数如下:
评委 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
评分/分 | 7.2 | 7.5 | 7.8 | 7.5 | 8.2 | 9.7 | 7.9 | 6.7 | 8.5 | 9.4 |
评分方案如下:
方案一:取各位评委所给分数的平均数,则该节目的得分为
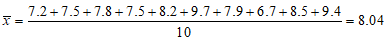 。
。
方案二:从评委所给的分数中先去掉一个最高分和一个最低分,再取其余八位评委所给分数的平均数,则该节目的得分为
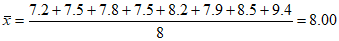 。
。
回答下列问题:
(1)小乐认为“方案二“比“方案一“更合理,你__________小乐的说法吗(填“同意”或”不同意”)?理由是________________;
(2)小乐认为评分既要突出专业评审的权威性又要尊重大众评审的喜爱度,因此设计了”方案三”:先计算1至4号评委所给分数的平均数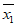 =7.5,5至10号评委所给分数的平均数
=7.5,5至10号评委所给分数的平均数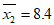 ,再根据比赛的需求设置相应的权重(
,再根据比赛的需求设置相应的权重(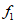 表示专业评委的权重,
表示专业评委的权重,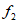 表示大众评委的权重,且
表示大众评委的权重,且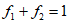 )。
)。
如
当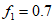 时,则
时,则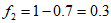 。
。
该节目的得分为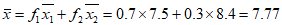 。
。
Ⅰ. 当按照”方案三”中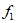 =0.6评分时,A节目的得分为___________;
=0.6评分时,A节目的得分为___________;
Ⅱ. 关于评分方案,下列说法正确的有___________。
①当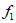 =0.5时,A节目按照“方案三“和“方案一“评分结果相同;
=0.5时,A节目按照“方案三“和“方案一“评分结果相同;
②当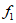 >0.4时,说明“方案三“评分更注重节目的专业性;
>0.4时,说明“方案三“评分更注重节目的专业性;
③当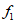 =0.3时,A节目按照“方案三“评分的结果比“方案一“和”方案二”都高。
=0.3时,A节目按照“方案三“评分的结果比“方案一“和”方案二”都高。
26. 在平面直角坐标系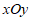 中,点A是抛物线
中,点A是抛物线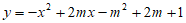 的顶点。
的顶点。
(1)求点A的坐标(用含m的代数式表示);
(2)若射线OA与x轴所成的锐角为45°,求m的值;
(3)将点P(0,1)向右平移4个单位得到点Q,若抛物线与线段PQ只有一个公共点,直接写出m的取值范围。
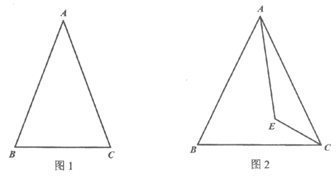
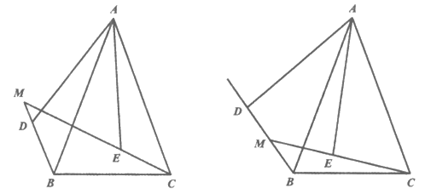
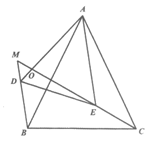
27. 在△ABC中,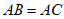 ,∠BAC=
,∠BAC=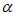 (0°<
(0°<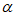 <60°),点E是△ABC内一动点,连接AE,CE,将△AEC绕点A顺时针旋转α,使AC边与AB重合,得到△ADB,延长CE与射线BD交于点M(点M与点D不重合)。
<60°),点E是△ABC内一动点,连接AE,CE,将△AEC绕点A顺时针旋转α,使AC边与AB重合,得到△ADB,延长CE与射线BD交于点M(点M与点D不重合)。
(1)依题意补全图1;
(2)探究∠ADM与∠AEM的数量关系为___________;
(3)如图2,若DE平分∠ADB,用等式表示线段MC,AE,BD之间的数量关系,并证明。
28. 在平面直角坐标系xOy中,对于点P和线段ST,我们定义点P关于线段ST的线段比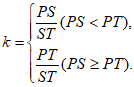
(1)已知点A(0,1),B(1,0)。
①点Q(2,0)关于线段AB的线段比k=_____________;
②点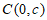 关于线段AB的线段比k=
关于线段AB的线段比k=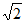 ,求c的值。
,求c的值。
(2)已知点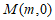 ,点
,点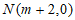 ,直线
,直线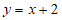 与坐标轴分别交于E,F两点,若线段EF上存在点使得这一点关于线段MN的线段比
与坐标轴分别交于E,F两点,若线段EF上存在点使得这一点关于线段MN的线段比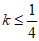 ,直接写出m的取值范围。
,直接写出m的取值范围。
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | D | D | B | B | B | C |
二、填空题(本题共16分,每小题2分)
9. 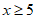 10.
10. 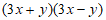 11.
11.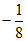
12. 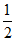 13. 25° 14.
13. 25° 14.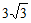
15. 答案不唯一,如:从2011年至2019年,该市常住人口逐年增加
16. 12
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 解:原式=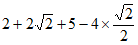 4分
4分
=7。 5分
18. 解:解不等式①,得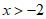 。 2分
。 2分
解不等式②,得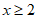 。 4分
。 4分
∴原不等式组的解集为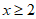 。 5分
。 5分
19. (1)补全图形如图所示:
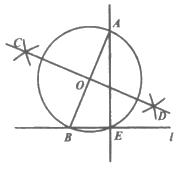 3分
3分
(2)OB; 4分
直径所对的圆周角是直角。 5分
20. (1)证明: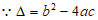 1分
1分
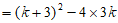
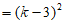 。
。
∵无论k取何值时,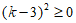 ,
,
∴原方程总有两个实数根。 2分
(2)解:∵原方程可化为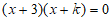 ,
,
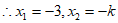 。(亦可用求根公式求出两根) 4分
。(亦可用求根公式求出两根) 4分
∵该方程有一个根大于1,
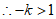 ,
,
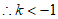 。 5分
。 5分
21. (1)证明:∵四边形ABCD是平行四边形,
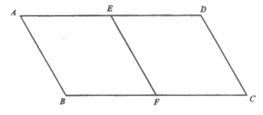
∴ AD∥BC,AD=BC,
∵E,F分别是AD,BC的中点,
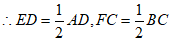 ,
,
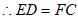 ,
,
∴四边形EFCD是平行四边形。
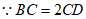 ,
,
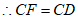 ,
,
∴四边形EFCD是菱形。 3分
(2)2; 4分
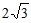 。 5分
。 5分
22. 解:(1)∵点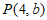 在直线
在直线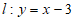 上,
上,
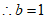 。 1分
。 1分
∵点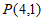 在函数
在函数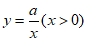 的图象上,
的图象上,
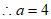 ,
,
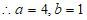 。 2分
。 2分
(2)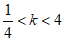 且
且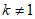 。 5分
。 5分
23. (1)证明:∵D为AC中点,
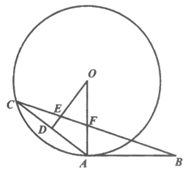
∴OD⊥AC,
∵AB是⊙O的切线,
∴OA⊥AB,
 ,
,
∴∠B=∠ACB,
∴∠AFB=∠DEC,
∵∠OFE=∠AFB,∠OEF=∠DEC,
∴∠OFE=∠OEF,
 。 3分
。 3分
(2)解:由(1)可证△CDE∽△BAF,
 ,
,
设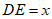 ,则
,则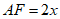 。
。
在Rt△OAD中,∠ODA=90°,sin∠AOD=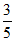 ,
,
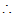 cos∠AOD=
cos∠AOD=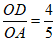 ,
,
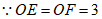 ,
,
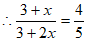 。
。
解得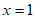 。(经检验,
。(经检验,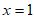 是所列方程的根)
是所列方程的根)
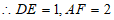 ,
,
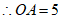 ,
,
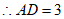 ,
,
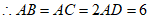 ,
,
在Rt△ABF中,∠FAB=90°,AF=2,AB=6,
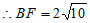 。 6分
。 6分
24. 解: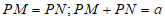 。 2分
。 2分
点P到DE的距离PH与a的数量关系为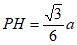 。 3分
。 3分
证明:连接PB,过点P作PH⊥DE于点H,
∵DP平分∠ADE,PM⊥BA,
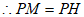 ,
,
易得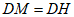 ,
,
同理可证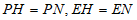 ,
,
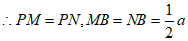 。
。
又∵PM⊥BA,PN⊥BC,
∴BP平分∠ABC,
在Rt△PMB中,∠PBM=30°,
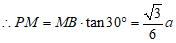 ,
,
即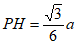 。 6分
。 6分
25. 解:(1)同意,平均数容易受到极端数据的影响; 2分
不同意,平均数与每一个数据都有关。 2分
(2)7.86; 4分
②③。 6分
26. 解:(1)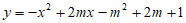
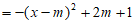 ,
,
∴顶点A的坐标为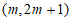 。 2分
。 2分
(2)∵射线OA与x轴所成的锐角为45°,
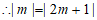 ,
,
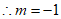 或
或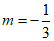 。 4分
。 4分
(3)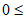
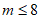 且
且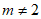 。 6分
。 6分
27. 解:(Ⅰ)补全图形如图所示(两种情况画出一种即可) 2分
(2)∠ADM=∠AEM或∠ADM+∠AEM=180°。 4分
(3)线段MC,AE,BD之间的数量关系是:MC=AE+BD。 5分
证明:由作图可知△ABD≌△ACE。
∴∠ADB=∠AEC,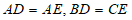 。
。
∴∠ADM=∠AEM,
∵DE平分∠ADB,
∴∠ADE=∠BDE,
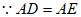 ,
,
∴∠ADE=∠AED,
∴∠BDE=∠AED,
∴AE∥BM,
∴∠DAE=∠ADM,∠AEM=∠M。
又∵∠AEM=∠ADM,
∴∠DAE=∠AEM,∠ADM=∠M,
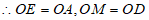 ,
,
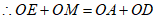 ,
,
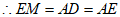 ,
,
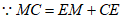 ,
,
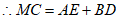 。 7分
。 7分
28. 解:(1)①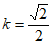 ; 1分
; 1分
②由题意得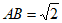 ,AB的垂直平分线交y轴于点O,
,AB的垂直平分线交y轴于点O,
当点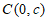 在点O上方时,
在点O上方时,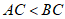 ,
,
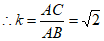 ,
,
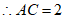 ,
,
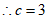 。
。
当点C在点O下方时,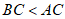 ,
,
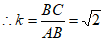 ,
,
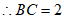 ,
,
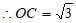
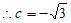 。
。
综上所述,c的值为3或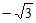 。 4分
。 4分
(2)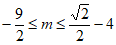 或
或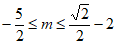 。 7分
。 7分

