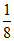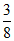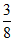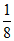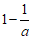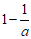本试卷满分为150分,考试时间为120分钟.
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
(1)已知集合A={1,3,5),B={x|x2-16<0},则A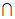 B=
B=
(A){1,3} (B){3,5} (C){1,3,5} (D)(0,4)
(2)下列函数中,是奇函数且最小正周期T=π的是
(A)
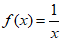 (B)
(B)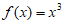
(C)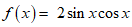 (D)
(D)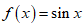
(3)复数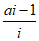 在复平面上对应的点位于第一象限,则实数a的取值范围是
在复平面上对应的点位于第一象限,则实数a的取值范围是
(A)(-∞,-1) (B)(-∞,0) (C)(0,+∞) (D)(1,+∞)
(4)一几何体的直观图和主视图如图所示,下列给出的四个俯视图中正确的是
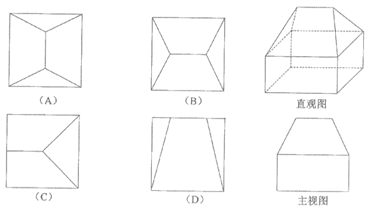
(5)”直线l垂直于平面α内无数条直线“是“直线l垂直于平面α”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(6)已知菱形ABCD的边长为a,∠ABC=60°,则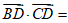
(A)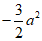 (B)
(B)
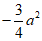 (C)
(C)
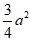 (D)
(D)
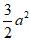
(7)过抛物线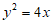 的焦点F的直线交抛物线于A、B两点,若F是线段AB的中点,则
的焦点F的直线交抛物线于A、B两点,若F是线段AB的中点,则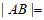
(A) 1 (B)2 (C)3 (D)4
(8)”回文数“是指从左到右读与从右到左读都一样的正整数.如22,121,3443等,那么在四位数中,回文数共有
(A) 81个 (B) 90个 (C) 100个 (D) 900个
(9)已知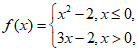 若
若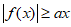 在x∈[-1,1]上恒成立,则实数a的取值范围是
在x∈[-1,1]上恒成立,则实数a的取值范围是
(A) (-∞,-1]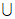 [0,+∞) (B)[0,1]
[0,+∞) (B)[0,1]
(C)[1,0] (D)(-1,0)
(10)瑞士著名数学家欧拉在1765年证明了定理:三角形的外心、重心、垂心位于同一条直线上,这条直线被后人称为三角形的“欧拉线“,在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线“与圆M:
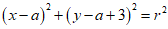 相切.则圆M上的点到直线x-y+3=0的距离的最小值为
相切.则圆M上的点到直线x-y+3=0的距离的最小值为
(A)
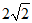 (B)
(B)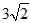 (C)
(C)
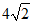 (D)6
(D)6
第二部分(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分.
(11)双曲线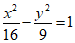 的离心率为___________.
的离心率为___________.
(12)已知函数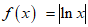 ,若
,若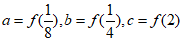 ,则a,b,c从小到大排序为________.
,则a,b,c从小到大排序为________.
(13)如图,如果每个横行上两数字之和相等,每个竖列上两个数字之和相等,请写出一组满足要求的不全相等的a11,a12,a21,a22的值.
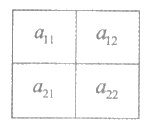
a11=__________, a12=________,a21=_________, a22=__________.
(14)在锐角△ABC中,a=
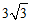 ,c=5,a=2bsinA,则B=___________,b=____________.
,c=5,a=2bsinA,则B=___________,b=____________.
(15)海水受日月的引力,会发生潮汐现象.在通常情况下,船在涨潮时驶入航道,进入港口,落潮时返回海洋,某兴趣小组通过AI技术模拟在一次潮汐现象下货船出入港口的实验:首先,设定水深y(单位:米)随时间x(单位:小时)的变化规律为y=0.8sin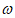 x+2(
x+2(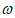 ∈R),其中0≤x≤
∈R),其中0≤x≤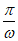 ;然后,假设某货船空载时吃水深度(船底与水面的距离)为0.5米,满载时吃水深度为2米,卸货过程中,随着货物卸载,吃水深度以每小时0.4米的速度减小;并制定了安全条例,规定船底与海底之间至少要有0.4米的安全间隙,在此次模拟实验中,若货船满载进入港口,那么以下结论正确的是__________.
;然后,假设某货船空载时吃水深度(船底与水面的距离)为0.5米,满载时吃水深度为2米,卸货过程中,随着货物卸载,吃水深度以每小时0.4米的速度减小;并制定了安全条例,规定船底与海底之间至少要有0.4米的安全间隙,在此次模拟实验中,若货船满载进入港口,那么以下结论正确的是__________.
①若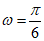 ,货船在港口全程不卸货,则该船在港口至多能停留4个小时;
,货船在港口全程不卸货,则该船在港口至多能停留4个小时;
②若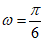 ,货船进入港口后,立即进行货物卸载,则该船在港口至多能停留4个小时;
,货船进入港口后,立即进行货物卸载,则该船在港口至多能停留4个小时;
③若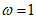 ,货船于x=1时进入港口后,立即进行货物卸载,则
,货船于x=1时进入港口后,立即进行货物卸载,则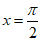 时,船底离海底的距离最大;
时,船底离海底的距离最大;
④若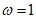 ,货船于x=1时进入港口后,立即进行货物卸载,则
,货船于x=1时进入港口后,立即进行货物卸载,则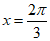 时,船底离海底的距离最大.
时,船底离海底的距离最大.
三、解答题共6小题,共85分,解答应写出文字说明,演算步骤或证明过程.
(16)(本小题13分)
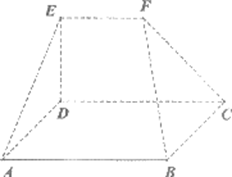
如图,在五面体ABCDEF中,面ABCD为正方形,面ABFE
 面CDEF= EF,AD⊥ED,CD⊥EA.
面CDEF= EF,AD⊥ED,CD⊥EA.
(I)求证:CD∥平面ABFE;
(II)若EF=ED,CD= 2EF=2,求平面ADE与平面BCF所成的锐二面角的大小.
(17)(本小题13分)
已知有限数列{an}共有30项,其中前20项成公差为d的等差数列,后11项成公比为q的等比数列,记数列的前n项和为Sn,从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(I)d,q的值;
(II)数列{an}中的最大项.
条件①:a2=4, S5=30,a21=20;
条件②:S3=0,a20=-36,a22=-9;
条件③:S1=48,a21=20,a24 =160.
注:如果选择多个条件分别解答,按第一个解答计分.
(18)(本小题14分)
某大型连锁超市的市场部为了比较线下、线上这两种模式的销售情况,从某地区众多门店中随机抽取8家门店,对其线下和线上这两种销售模式下的日营业额(单位:万元)进行调查.调查结果如下:
门店1 | 门店2 | 门店3 | 门店4 | 门店5 | 门店6 | 门店7 | 门店8 | |
线下日营业额 | 9 | 6.5 | 19 | 9.5 | 14.5 | 16.5 | 20.5 | 12.5 |
线上日营业额 | 11.5 | 9 | 12 | 17 | 19 | 23 | 21.5 | 15 |
若某门店一种销售模式下的日营业额不低于15万元,则称该门店在这种销售模式下的日营业额达标;否则就称该门店在此种销售模式下的日营业额不达标.
若某门店的日营业总额(线上和线下两种销售模式下的日营业额之和)不低于30万元,则称该门店的日营业总额达标;否则就称该门店的日营业总额不达标.
(I)从8个样本门店中随机抽取3个,求抽取的3个门店的线下日营业额均达标的概率;
(II)若从该地区众多门店中随机抽取3个门店,记随机变量X表示抽到的日营业总额达标的门店个数.以样本门店的日营业总额达标的频率作为一个门店的日营业总额达标的概率,求X的分布列和数学期望;
(III)线下日营业额和线上日营业额的样本平均数分别记为μ1和μ2,线下日营业额和线上日营业额的样本方差分别记为S12和S22.试判断μ1和μ2的大小,以及S12和S22的大小.(结论不要求证明)
(19)(本小题15分)
已知椭圆C: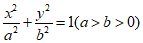 的右焦点为F(1,0),且经过点A(-2,0)和点B(2,0).
的右焦点为F(1,0),且经过点A(-2,0)和点B(2,0).
(I)求椭圆C的方程;
(II)M和N是椭圆C上两个不同的点,四边形AMBN是平行四边形,直线AM、AN分别交y轴于点P和点Q,求四边形APFQ面积的最小值.
(20)(本小题15分)
已知函数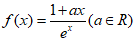 .
.
(I)当a=-1时,求f(x)在x=0处的切线方程;
(II)已知f(x)≤1对任意x∈R恒成立,求a的值.
(21)(本小题15分)
由m个正整数构成的有限集M={a1,a2,a3,…,an}(其中a1<a2<a3<…<am),记P(M)=a1+a2+…+am,特别规定P(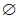 )=0,若集合M满足:对任意的正整数k≤P(M),都存在集合M的两个子集A,B,使得k = P(A) – P(B)成立,则称集合M为“满集“.
)=0,若集合M满足:对任意的正整数k≤P(M),都存在集合M的两个子集A,B,使得k = P(A) – P(B)成立,则称集合M为“满集“.
(I)分别判断集合M1={1,2}与M2={2,3}是否为“满集“,请说明理由;
(Ⅱ)若集合M为“满集“,求a1的值;
(Ⅲ)若a1,a2,a3,…,am是首项为1公比为2的等比数列,判断集合M是否为“满集“,并说明理由.
参考答案
一、选择题:本大题共10个小题,每小题4分,共40分.
题号 | (1) | (2) | (3) | (4) | (5) 5 | (6) | (7) | (8) | (9) | (10) |
答案 | A | C | C | B | B | D | D | B | C | A |
二、填空题:本大题共5个小题,每小题5分,共25分.
(11)
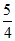 ; (12) c<b<a (13) 1,2,2,1 答案不唯一;
; (12) c<b<a (13) 1,2,2,1 答案不唯一;
(14)
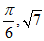
(15)①④.
三、解答题:本大题共6个小题,共85分.解答题应写出文字说明,证明过程或演算步骤.
(16)(本小题13分)
解:(I)在五面体ABCDEF中,
因为面ABCD是正方形,
所以CD∥AB.
又因为AB
 平面ABFE,
平面ABFE,
CD
 平面ABFE,
平面ABFE,
所以CD∥平面ABFE.
(Ⅱ)因为面ABCD是正方形,所以CD⊥AD.
又因为CD⊥AE.
又AD
 AE=A,
AE=A,
所以CD⊥平面ADE.
又因为DE
 平面ADE,
平面ADE,
所以CD⊥DE.
因为面ABCD是正方形,
所以CD⊥AD.
又因为AD⊥DE,
所以以点D为坐标原点,DA,DC,DE分别为x,y,z轴,
如图建立空间直角坐标系.
因为CD=2EF=2,EF=ED
D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),E(0,0,1).
由(I) CD∥平面ABFE,CD
 平面CDEF,
平面CDEF,
平面CDEF
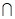 平面ABFE=EF,
平面ABFE=EF,
所以CD∥EF.
所以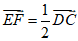 .
.
可得F(0,1,1).
由题意知平面ADE的法向量为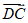 =(0,2,0).
=(0,2,0).
设平面BCF的法向量为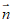 =(x,y,z).
=(x,y,z).
由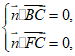 得
得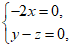
令y=1,得z=1,x=0,所以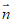 =(0,1,1).
=(0,1,1).
设平面ADE与平面BCF所成锐二面角为θ.
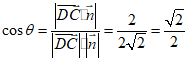
所以平面ADE与平面BCF所成锐二面角为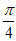 .
.
(17)(本小题13分)
选择条件①:a2=4,S5=30,a21=20
解:(I)因为{an}的前20项成等差数列,a2 =4,S5=30,
所以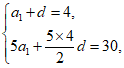 ,解得
,解得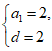
所以a20 =2+19×2=40.
因为数列{an}后11项成公比为q的等比数列,
所以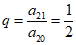
综上,d=2,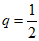 .
.
(II){an}的前20项成等差数列,d>0.
所以前20项为递增数列.
即:前20项的最大项为a20=40.
数列{an}的后11项成等比数列,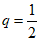 ,
,
所以后11项是递减数列.
即:后11项的最大项为a20=40.
综上,数列{an}的最大项为第20项,其值为40.
选择条件②:S3 =0,a20=-36,a22=-9
解:(I)因为{an}的前20项成等差数列,S3 =0,a20=-36,
所以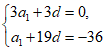 ,所以
,所以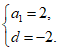
因为数列{an}后11项成公比为q的等比数列,
a20=-36,又因为a22=-9,
所以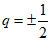 .
.
综上,d=-2,
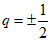
(II){an}的前20项成等差数列,d<0.
所以前20项为递减数列,
前20项的最大项为a1=2.
因为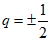
i.当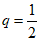 时,
时,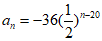 (20≤n≤30且n∈N*),
(20≤n≤30且n∈N*),
所以当20≤n≤30时,an<0.
此时,数列{an}的最大项为第1项,其值为2;
ii.当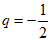 时,
时,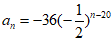 (20≤n≤30且n∈N*),
(20≤n≤30且n∈N*),
后11项的最大项为a21=18.
此时,数列{an}的最大项为第21项,其值为18.
综上,当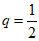 时,数列{an}的最大项为第1项,其值为2;
时,数列{an}的最大项为第1项,其值为2;
当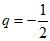 时,数列{an}的最大项为第21项,其值为18.
时,数列{an}的最大项为第21项,其值为18.
选择条件③:S1=48,a21= 20,a24 =160
解:(I)因为数列{an}后11项成公比为q的等比数列,a21=20,a24=160,
所以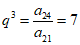 ,解得q=2.
,解得q=2.
所以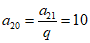 .
.
又因为{an}的前20项成等差数列,S1=a1=48,
所以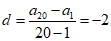 .
.
综上,d= -2,q=2.
(Ⅱ){an}的前20项成等差数列,d<0.
所以前20项为递减数列.
前20项的最大项为a1=48.
{an}的后11项成等比数列,而a20=10,q=2,
an=10·2n-20(20≤n≤30且n∈N*),
所以后11项为递增数列,
后11项的最大项为a30 =10240,
综上,数列{an}的最大项为第30项,其值为10240.
(18)(本小题14分)
解:(I)设“抽取的3个门店的线下日营业额均达标“为事件A,由题意知,8个样本门店中线下日营业额达标的有3家,
所以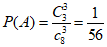 .
.
所以抽取的3个门店的线下日营业额均达标的概率为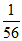 .
.
(II)由题意,8个样本门店中线下日营业总额达标的有4家,
所以从该地区众多门店中任选1个门店,日营业总额达标的概率为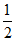 .
.
依题意,随机变量X的所有可能取值为0,1,2,3.
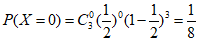 ;
;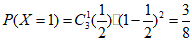
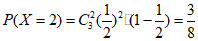 ;
;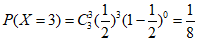
所以随机变量X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
其数学期望
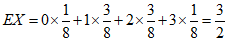 .
.
(III)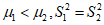
(19)(本小题15分)
解:(I)由已知a=2,c=1,
所以b2= a2-c2=3.
所以椭圆C的方程为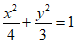 .
.
(II)因为四边形AMBN是平行四边形,
所以AB与MN的中点重合,所以M、N关于原点对称,
设M (x1,y1),则N(-x1,-y1).(x1≠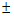 2且y1≠0)
2且y1≠0)
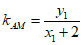 ,
,
直线AM的方程为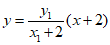 ,
,
令x=0,得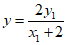 ,即
,即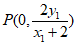 ,
,
又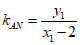
直线AN的方程为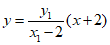
令x=0,得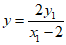 ,即
,即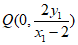 ,
,
四边形APFQ面积为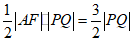 ,
,
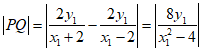
因为点M在椭圆上,
所以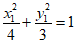 ,
,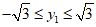 且
且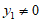
所以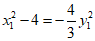
所以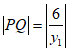
所以当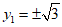 时,
时,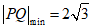
所以四边形APFQ面积的最小值为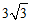 .
.
(20)(本小题15分)
解:(I)当a=-1时,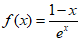 ,
,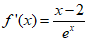 ,
,
所以f(0)=1,f'(0)=-2
切线 的斜率为k=f'(0)=-2.
的斜率为k=f'(0)=-2.
所以f (x)在x=0处的切线方程为y=-2x+1.
(II)依题意,f(x)≤1对任意x∈R恒成立,
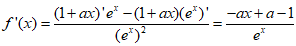
当a=0时,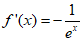 ,由于
,由于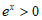 ,则f’(x)<0恒成立,
,则f’(x)<0恒成立,
所以f(x)在R内单调递减,
因为f(0)=1,故当x<0时,f(x)>1,不符合题意,
当a≠0时,令f'(x)=0,得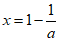
那么x,f'(x),f(x)的变化情况如下表:
x | (-∞, |
| ( |
f'(x) | – | 0 | + |
f(x) | 单调递减 | 极小值 | 单调递增 |
当a<0时,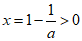 ,因为f(0)=1,
,因为f(0)=1,
所以结合f(x)的单调性知:当x<0时,f(x)>1,不符合题意,
当0<a<1时,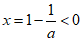 ,因为f(0)=1,
,因为f(0)=1,
所以结合f(x)的单调性知当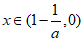 时,f(x)>1,不符合题意.
时,f(x)>1,不符合题意.
当a>1时,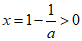 ,因为f(0)=1,
,因为f(0)=1,
所以结合f(x)的单调性知当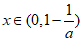 时,f(x)>1,不符合题意.
时,f(x)>1,不符合题意.
当a=1时,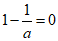
由f(x)的单调性可知,f(x)min=f(0)=1,所以符合题意,
综上,a=1.
(21)(本小题15分)
解:(I)M1是满集,M2不是满集.
P(M1)=3,且M1的子集为 ,{1},{2},{1,2}
,{1},{2},{1,2}
k=1,k=P({1}-P( ),k=2,k=P({2})-P(
),k=2,k=P({2})-P( ),k=3,k=P({1,2}) – P(
),k=3,k=P({1,2}) – P(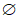 )
)
所以M1是满集;
P(M2)=5,且M2的子集为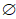 ,{2},{3},{2,3}
,{2},{3},{2,3}
k=4时不存在集合M的两个子集A、B,使得4=P(A)-P(B)成立,
所以M2不是满集.
(II)设k0=P(M),因为集合M为“满集“对任意的正整数k≤P(M),都存在集合M的两个子集A、B,使得k=P(A)-P(B)成立.
则k0-1= P(A) – P(B),且P(B)≥0,所以P(A)= k0或P(A)=k0-1.
当P(A)=k0时P(B)=1,此时a1=1;
当P(A)=k0-1时P(B)=0,因为a1<a2<a3<…<am,
所以a2+…+am为最大k0-1,此时a1=1.
综上a1=1.
(III)集合M是满集,
由题意知集合M={1,2,4,…,2m-1},P(M)=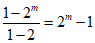 ,
,
对任意的正整数k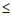 2m-1,根据二进制可知,
2m-1,根据二进制可知,
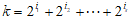 (0≤is<…<i1<m).
(0≤is<…<i1<m).
取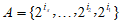 ,B=
,B=
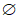 .
.
即k= P(A) – P(B),所以集合M为“满集“,
【若有不同解法,请酌情给分】