北京101中学2020-2021学年下学期高二年级期末考试数学试卷
一、选择题:共10小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1.若全集U=R,A={x|x<1},B={x|x>−1},则( )
(A)A⊆B (B)B⊆A (C)B⊆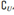 A (D)
A (D)
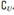 A⊆B
A⊆B
2.下列数列中,156是其中一项的是( )
(A){n2+1} (B){n2−1} (C){n2+n} (D){n2+n−1}
3.若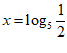 ,
,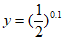 ,
,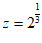 ,则( )
,则( )
(A)x<z<y (B)x<y<z (C)y<x<z (D)z<x<y
4.已知a,b,c满足c<b<a,且ac<0,那么下列选项中不一定成立的是( )
(A)ab>ac (B)c(b−a)>0 (C)cb2<ab2 (D)ac(a−c)<0
5.已知x>0,y>0,且x+y=8,则(x+1)(y+1)的最大值为( )
(A)9 (B)16 (C)25 (D)36
6.设a∈R,若关于x的不等式x2−ax+1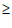 0在区间[1,2]上有解,则( )
0在区间[1,2]上有解,则( )
(A)a≤2 (B)
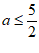 (C)a≥2 (D)
(C)a≥2 (D)
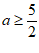
7.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数α满足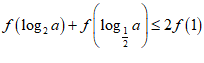 ,则α的取值范围是( )
,则α的取值范围是( )
(A)[
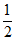 ,+∞) (B)[
,+∞) (B)[
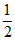 ,1) (C)[
,1) (C)[
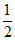 ,2] (D)(0,2]
,2] (D)(0,2]
8.设Sn是等差数列{an}的前n项和,且S6>S7>S5,则下列结论正确的是( )
(A)S11>0 (B)S12<0 (C)S13>0 (D)S8>S6
9.已知函数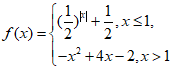 若关于x的方程a=f(x)恰有两个不同实根,则实数a的取值范围是( )
若关于x的方程a=f(x)恰有两个不同实根,则实数a的取值范围是( )
(A)(−∞,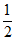 )∪[1,2) (B)(0,
)∪[1,2) (B)(0,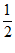 )∪[1,2 ) (C)(
)∪[1,2 ) (C)(
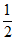 ,1)∪(
,1)∪(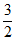 ,2) (D)(
,2) (D)(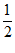 ,2)
,2)
10.关于函数f(x)=sinx−xcosx,下列说法错误的是( )
(A)f(x)是奇函数 (B)0不是f(x)的极值点
(C)f(x)在(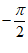 ,
,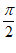 )上有且仅有3个零点 (D)f(x)的值域是R
)上有且仅有3个零点 (D)f(x)的值域是R
二、填空题:共5小题。
11.若集合A={x|−1≤2x+1≤3},B={x|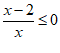 },则A∩B=_________.
},则A∩B=_________.
12.写出“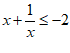 “成立的一个充分不必要条件_________.
“成立的一个充分不必要条件_________.
13.已知函数f(x),g(x)分别由下表给出:
x | 1 | 2 | 3 |
f(x) | 1 | 3 | 1 |
x | 1 | 2 | 3 |
g(x) | 3 | 2 | 1 |
满足f[g(x)]>g[f(x)]的x的值是_________.
14.已知f(x)=ln(x2+1),g(x)=(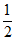 )x−m,若∀x1∈[0,3],∃x2∈[1,2],使得f(x1)
)x−m,若∀x1∈[0,3],∃x2∈[1,2],使得f(x1)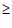 g(x2),则实数m的取值范围是_________.
g(x2),则实数m的取值范围是_________.
15.数列{an}中,如果存在ak,使得“ak>ak−1且ak>ak+1“成立(其中k≥2,k∈N∗),则称ak为{an}的一个峰值.
(1)若an=−3n2+11n,则{an}的峰值为_________;
(2)若an=−3n2+tn,且{an}不存在峰值,则实数t的取值范围是_________.
三、解答题:共4小题。解答应写出文字说明、演算步骤或证明过程。
16.已知函数f(x)=x2+a,x∈R.
(1)对任意x1,x2∈R,比较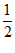 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(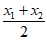 )的大小;
)的大小;
(2)若x∈[−1,1],都有|f(x)|≤1,求实数a的取值范围.
17.已知等比数列{an}的首项为2,等差数列{bn}的前n项和为Sn,且a1+a2=6,2b1+a3=b4,S3=3a2.
(1)求{an},{bn}的通项公式;
(2)设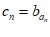 ,求数列{cn}的前n项和.
,求数列{cn}的前n项和.
18.已知函数f(x)=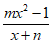 是奇函数,且f(2)=
是奇函数,且f(2)=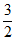 .
.
(1)求实数m,n的值;
(2)设函数g(x)=f(x)+1,曲线y=g(x)在点P(t,g(t))(t≥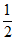 )处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的单调区间及最值.
)处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的单调区间及最值.
19.若函数f(x)满足:对于s,t∈[0,+∞),都有f(s) ≥0,f(t) ≥0,且f(s)+f(t)≤f(s+t),则称函数f(x)为“T函数“
(1)试判断函数f1(x)=x2与f2(x)=ln(x+1)是否是“T函数“,并说明理由;
(2)设函数f(x)为“T函数“,且存在x0∈[0,+∞),使f(f(x0))=x0,求证:f(x0)=x0;
(3)试写出一个“T函数“,满足f(2)=4,且使集合{y|y=f(x),0≤x≤2}中元素的个数最少(只需写出你的结论).
参考答案
1.(2020海淀二模1)D
2.C
3.B
4.(2004高考北京理6)C
5.C
6.B
7.C
8.A
9.C
10.(2018海淀二模理6)C
A.f(−x)=sin(−x)−(−x)cos(−x)=−sinx+xcosx=−f(x),即f(x)为奇函数,故A正确;
B.f‘(x)=cosx−(cosx−xsinx)=xsinx,f′(0)=0,
当x∈(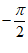 ,0)时,f′(x)>0,所以f(x)在(
,0)时,f′(x)>0,所以f(x)在(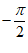 ,0)单调递增,
,0)单调递增,
当x∈(0,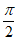 )时,f′(x)>0,所以f(x)在(0,
)时,f′(x)>0,所以f(x)在(0,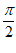 )单调递增,
)单调递增,
所以x=0不是极值点,故B正确;
C.f′(x)=xsinx,当x∈(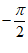 ,
,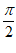 )时,f′(x)≥0,f(x)在区间(
)时,f′(x)≥0,f(x)在区间(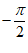 ,
,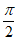 )上单调递增,
)上单调递增,
又因为f(0)=0,所以f(x)在区间(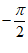 ,
,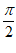 )上只存在一个零点,故C错;
)上只存在一个零点,故C错;
D.f(x)在R上连续,当x=2kπ(k∈Z)时,f(2kπ)=sin2kπ−2kπcos2kπ=−2kπ,
所以f(x)的值域为R,故D正确.
11.(0,1].
12.(2019石景山高三上期末理12)x=−2(答案不唯一).
13.2.
14.[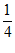 ,+∞).
,+∞).
15.(2012海淀高三上期中理(改编)14)10;{t|t≤9或t=6n+9,n∈N∗}.
16.f(x)=x2+a.
(1)
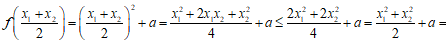
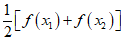 ,
,
所以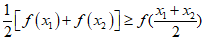 ,当且仅当x1=x2时取到等号.
,当且仅当x1=x2时取到等号.
(2)|f(x)|≤1在[−1,1]恒成立;−1≤f(x) ≤1在[−1,1]恒成立;
又f(x)对称轴是x=0,且开口向上;
fmax(x)=max{f(−1),f(0),f(1)};fmin(x)=min{f(−1),f(0),f(1)};
−1≤f(x) ≤1在[−1,1]恒成立等价于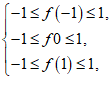 所以
所以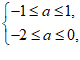
所以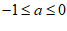 ,即a的取值范围是[−1,0].
,即a的取值范围是[−1,0].
17.(2019东城一模文16)
(1)设数列{an}的公比为q,数列{bn}的公差为d.
由a1+a2=6,得a1+a1q=6.因为a1=2,所以q=2.
所以an=a1qn−1=2·2n−1=2n.
由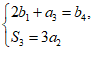 得
得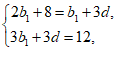 解得
解得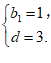
所以bn=b1+(n−1)d=3n−2.
(2)由(1)知an=2n,bn=3n−2.所以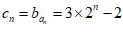 .
.
从而数列{cn}的前n项和
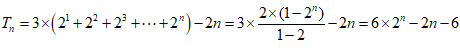 .
.
18.(1)f(x)是奇函数,且f(2)=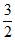 ,所以f(−2)=
,所以f(−2)=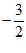 ,
,
从而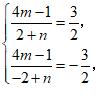 解得
解得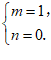
经检验,此时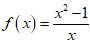 是奇函数.
是奇函数.
所以m=1,n=0.(2)g(x)=f(x)+1=x−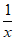 +1,g′(x)=1+
+1,g′(x)=1+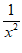 ,切点P(t,t−
,切点P(t,t−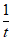 +1)(
+1)(
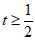 ).
).
切线斜率k=1+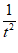 ,
,
切线方程为y−(t−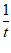 +1)=(1+
+1)=(1+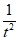 )(x−t),即y=(1+
)(x−t),即y=(1+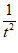 )x−
)x−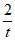 +1,
+1,
与两数轴的交点为(0,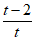 )和(
)和(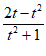 ,0).
,0).
由于切线与坐标轴围成三角形,t≠2,
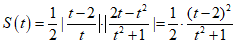 ,其中
,其中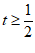 且t≠2,
且t≠2,
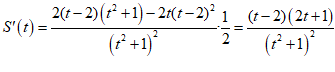 .
.
因为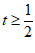 且t≠2,所以:
且t≠2,所以:
t | [ | (2,+∞) |
S′(t) | − | + |
S(t) | ↘ | ↗ |
S(t)单调增区间为(2,+∞),单调减区间为[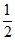 ,2),无极值.
,2),无极值.
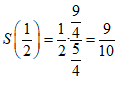 ,
,
且当t>2时,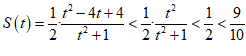 ,
,
当t∈(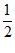 ,2)时,S(t)<S(
,2)时,S(t)<S(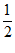 )=
)=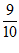 ,
,
所以S(t)的最大值为S(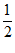 )=
)=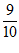 .
.
由S(t)在区间(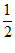 ,2)和区间(2,+∞)上的连续性知,S(t)无最小值.
,2)和区间(2,+∞)上的连续性知,S(t)无最小值.
19.(1)f1(x)=x2是T函数,f2(x)=ln(x+1)不是T函数,理由如下:
对于f1(x)=x2,∀s,t∈[0,+∞),都有f1(s)≥0,f1(t) ≥0,
f1(s)+f1(t)−f1(s+t)=s2+t2−(s+t)2=−2st≤0,f1(s)+f1(t)
≤f1(s+t),
所以f1(x)=x2是T函数.
当s>0,t>0时,f2(s)+f2(t)−f2(s+t)=ln(s+1)+ln(t+1)−ln(s+t+1)=ln(1+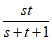 ).
).
因为s>0,t>0,所以f2(s)+f2(t)−f2(s+t)=ln(1+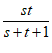 )>0,
)>0,
不满足f2(s)+f2(t)≤f2(s+t),所以f2(x)=ln(x+1)不是T函数.
(2)设x1,x2∈[0,+∞),x2>x1,设∆x=x2−x1,则∆x>0,x1>0.
由已知得:f(x2)=f(x1+∆x)≥f(x1)+f(∆x) ≥f(x1).
若存在x0∈[0,+∞),使得f(f(x0))=x0,
若f(x0)>x0,则f(f(x0)) ≥f(x0)>x0,与f(f(x0))=x0矛盾;
若f(x0)<x0,则f(f(x0))≤f(x0)<x0,与f(f(x0))=x0矛盾.
综上f(f(x0))=x0.
(3)
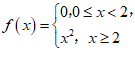 .(答案不唯一)
.(答案不唯一)