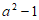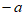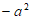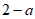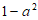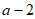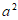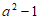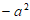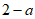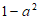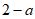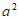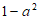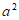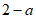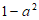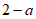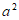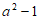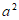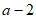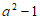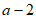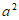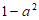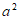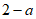本试卷有三道大题,考试时长120分钟,满分150分。
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合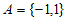 ,集合
,集合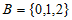 ,那么
,那么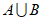 =
=
A. 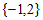 B. {1} C.
B. {1} C. 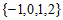 D.
D.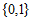
2. 已知向量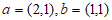 ,则向量
,则向量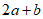 =
=
A. (5,3) B. (4,4) C. (5,4) D. (4,5)
3. 某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从甲种型号的产品中抽取的件数为
A. 24 B. 18 C. 15 D. 12
4. 甲、乙两人参加一个面试,通过面试的概率分别为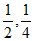 ,且甲、乙两人是否通过互不影响,则两人均未通过面试的概率是
,且甲、乙两人是否通过互不影响,则两人均未通过面试的概率是
A. 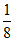 B.
B. 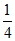 C.
C. 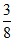 D.
D.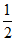
5. 某菜市居民中随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图,则可估计该市居民该月用水量在2.5立方米以上的概率是
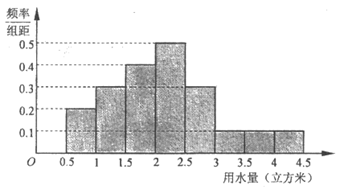
A. 0.7B. 0.6 C. 0.3 D. 0.15
6. 已知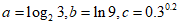 ,则
,则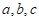 的大小关系为
的大小关系为
A. 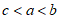 B.
B. 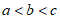 C.
C. 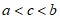 D.
D.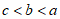
7. 函数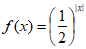 的值域是
的值域是
A. 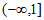 B.
B. 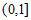 C.
C. 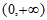 D.
D.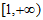
8. 设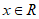 ,则”
,则”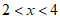 “是”
“是”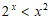 “的
“的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
9. 已知四个函数①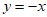 ②
②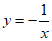 ③
③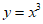 ④
④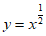 ,从中任选2个,事件”所选2个函数的图像至多有1个公共点“的概率是
,从中任选2个,事件”所选2个函数的图像至多有1个公共点“的概率是
A. 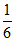 B.
B. 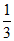 C.
C. 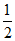 D.
D.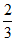
10. 若函数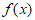 满足条件:对任意
满足条件:对任意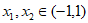 ,都有
,都有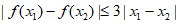 成立,则称
成立,则称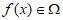 ,下列函数中属于
,下列函数中属于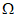 的是
的是
A. 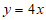 B.
B. 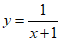 C.
C. 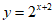 D.
D.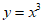
二、填空题:共5小题,每小题5分,共25分。
11. 函数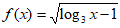 的定义域为_________________。
的定义域为_________________。
12. 计算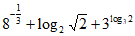 =_________________。
=_________________。
13. 已知函数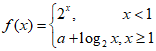 ,若
,若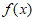 在R上单调递增,则a的取值范围是________________。
在R上单调递增,则a的取值范围是________________。
14. 已知函数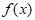 满足
满足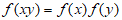 ,且
,且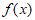 在区间
在区间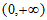 上单调递减,则
上单调递减,则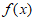 可以是_________________________。
可以是_________________________。
15. 已知△ABC,下列命题正确的是______________。
①若点P满足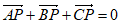 ,则点P为△ABC的外心;
,则点P为△ABC的外心;
②若点P满足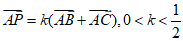 ,则点P在BC边的中线上;
,则点P在BC边的中线上;
③若点P满足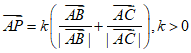 ,则点P在∠BAC的角平分线上。
,则点P在∠BAC的角平分线上。
(本题给出的结论中,有多个符合题目要求,全部选对得5分,不选或错选得0分,其他得3分。)
三、解答题:共6小题,共85分,解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
已知向量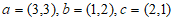 。
。
(Ⅰ)求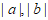 ;
;
(Ⅱ)若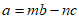 ,求实数
,求实数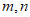 的值;
的值;
(Ⅲ)若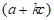 ∥
∥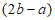 ,求实数k的值。
,求实数k的值。
17.(本小题13分)
已知函数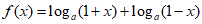 (a为常数,
(a为常数,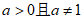 )。
)。
(Ⅰ)求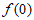 ;
;
(Ⅱ)判断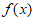 的奇偶性,说明理由;
的奇偶性,说明理由;
(Ⅲ)若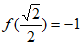 ,求使
,求使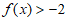 成立的x的取值范围。
成立的x的取值范围。
18. (本小题14分)
某校为了解高一年级学生对古诗词掌握的情况,举办高一年级古诗词朗诵比赛,对高一年级全体学生进行了两轮测试,并把两轮测试成绩的平均分作为比赛的最终成绩,现随机选取10名学生,成绩记录的数据如下:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | |
第一轮 测试成绩 | 96 | 90 | 89 | 87 | 92 | 89 | 87 | 90 | 92 | 90 |
第二轮 测试成绩 | 90 | 89 | 89 | 89 | 88 | 88 | 96 | 92 | 89 | 92 |
(Ⅰ)从该校高一年级学生中随机选取一名学生,试估计这名学生最终成绩大于等于90分的概率;
(Ⅱ)从上表最终成绩大于等于90分的学生中随机抽取两名学生,求这两名学生两轮测试成绩均大于等于90分的概率;
(Ⅲ)记上表的10名学生第一轮测试成绩的平均数和方差分别为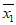 ,
,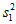 ,最终成绩的平均数和方差分别为
,最终成绩的平均数和方差分别为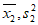 ,试比较
,试比较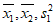 与
与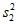 的大小。(只需写出结论)
的大小。(只需写出结论)
19. (本小题15分)
设函数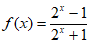 。
。
(Ⅰ)求方程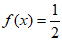 的根;
的根;
(Ⅱ)若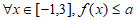 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)若方程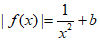 恰有两个实根,直接写出实数b的取值范围。
恰有两个实根,直接写出实数b的取值范围。
20. (本小题15分)
某电商平台为获取更多的新用户,对所售商品开展砍价活动,即一位消费者将购买商品的链接发给朋友后,每个朋友点击一次该链接就完成了一次砍价,直到链接中显示的剩余价格为0时,该消费者可以免费获得此商品。
设f(x)为砍价x次后商品的剩余价格(单位:元),精确到0.01,在砍价过程中,砍价算法分为三个阶段:
第一阶段为指数砍价阶段,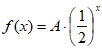 ,其中A为商品的初始价格,当
,其中A为商品的初始价格,当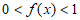 时,该阶段停止,并进入第二阶段;
时,该阶段停止,并进入第二阶段;
第二阶段为波动砍价阶段,此阶段砍价总金额不超过0.5元,可至多进行10个循环,每个循环内砍价3次,每次只能砍0.01元或0.02元,其中可砍0.01元一次、0.02元两次,顺序不定;
第三阶段为线性砍价阶段,每次只能砍价0.01元,直到剩余价格为0元时,结束砍价。
其中,在进行第二或第三阶段砍价时,若受邀用户为新用户,则享有0.3元的砍价特权,此特权不能跨越两个阶段,例如当第二阶段还剩0.15元时,新用户只能砍0.15元;当第三阶段不足0.3元时,直接砍为0元。
己知某商品的初始价格为768元。
(Ⅰ)求经过多少次砍价后可进入第二阶段,并求此时的剩余价格;
(Ⅱ)若进入第二阶段后只邀请新用户砍价,则需要多少个新用户才能完成砍价?
(Ⅲ)若第一阶段结束后,只能邀请一位新用户砍价,其他都邀请老用户,则最少还需要多少个老用户才能完成砍价?
21. (本小题15分)
设A是由m×n个实数组成的m行n列的数表,如果某一行(或某一列)各数之和为负数,则将该行(或该列)中所有数均变为原来的相反数,称为一次”操作”。
(Ⅰ)数表A如表1所示,若经过两次”操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次”操作”后所得的数表(写出一种方法即可);
1 | 2 | 3 | -7 |
-2 | 1 | 0 | 1 |
表1
(Ⅱ)数表A如表2所示,若必须经过两次”操作”才可使得到的数表每行的各数之和与每列的各数之和均为非负实数,求整数a的所有可能值;
a |
|
|
|
|
|
|
|
表2
(Ⅲ)对由m×n个实数组成的m行n列的任意一个数表A,能否经过有限次”操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由。
【试题答案】
一、选择题:共10小题。每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
C | A | D | C | C | A | B | A | D | D |
二、填空题:共5小题,每小题5分,共25分。
11. 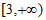 12. 3 13.
12. 3 13. 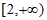 14.
14.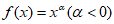
15. ②③
三、解答题:共6小题,共85分,解答应写出文字说明,演算步骤或证明过程。
16. 解:(Ⅰ)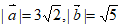
(Ⅱ)由题意得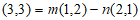 ,
,
所以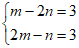 ,得
,得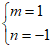
(Ⅲ)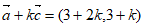
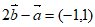
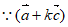 ∥
∥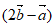
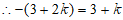
解得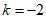 。
。
17. 解:(Ⅰ)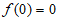 ;
;
(Ⅱ)由函数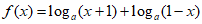 有意义,得
有意义,得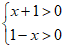 ,
,
所以函数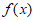 的定义域为
的定义域为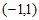 ,关于原点对称。
,关于原点对称。
因为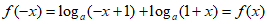 ,
,
所以函数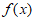 为偶函数。
为偶函数。
(Ⅲ)由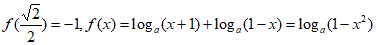 ,得
,得
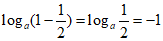 ,解得
,解得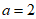 ;
;
所以,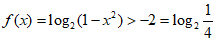 ,
,
由于函数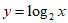 在
在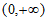 上单调增,
上单调增,
所以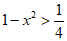 ,解得
,解得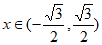 。
。
18. 解:(Ⅰ)这10名学生的考核成绩(单位:分)分别为:
93,89.5,89,88,90,88.5,91.5,91,90.5,91。
其中大于等于90分的有1号、5号、7号、8号、9号、10号,共6人。
所以样本中学生考核成绩大于等于90分的频率为: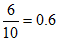 ,
,
从该校高一年级随机选取一名学生,
估计这名学生考核成绩大于等于90分的概率为0.6。
(Ⅱ)设事件A:从上述考核成绩大于等于90分的学生中再随机抽取两名同学,
这两名同学两轮测试成绩均大于等于90分。
由(Ⅰ)知,上述考核成绩大于等于90分的学生共6人,
其中两轮测试成绩均大于等于90分的学生有1号,8号,10号,共3人。
所以,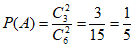 。
。
(Ⅲ)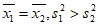 。
。
19. 解:(Ⅰ)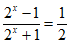
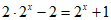
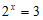
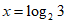
(Ⅱ)若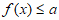 在
在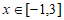 上恒成立
上恒成立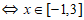 时,
时,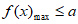
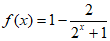 在R上是增函数。
在R上是增函数。
当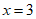 时,
时,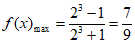
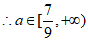
(Ⅲ)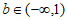
20. 解:(Ⅰ)由题意得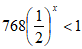 ,
,
两侧以2为底取对数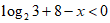 ,即
,即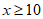 ,
,
即经过10次砍价进入第二阶段,
此时的价格为0.75元。
(Ⅱ)第二阶段一共有0.5元的价格区间,如用新用户则需要两个新用户砍完。
(i)此时进入第二阶段的价格为0.75元,
则第二阶段结束后还剩下0.25元,只需一个新用户即可,
故共需要3位新用户。
(ii)若此新用户处于第二阶段,其最多可以相当于18个老用户;
若此新用户处于第三阶段,则其最多相当于25个新用户。
因此要追求使用老用户最少,则新用户必须在第三阶段第一个入场,
此时需要老用户填满第二阶段共10×3=30个。
21. (Ⅰ)解法1:

法2:

法3:

(Ⅱ)每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1;
①如果首先操作第三列,则
a |
| a |
|
|
|
|
|
则第一行之和为2a-1,第二行之和为5-2a,
这两个数中,必须有一个为负数,另外一个为非负数,
所以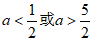
当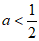 时,则接下来只能操作第一行,
时,则接下来只能操作第一行,
-a |
| -a |
|
|
|
|
|
此时每列之和分别为: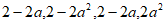
必有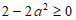 ,解得
,解得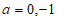
当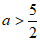 时,则接下来操作第二行
时,则接下来操作第二行
a |
| a | - |
|
|
| - |
此时第4列和为负,不符合题意。
②如果首先操作第一行
-a |
| a |
|
|
|
|
|
则每一列之和分别为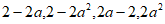
当a=1时,每列各数之和已经非负,不需要进行第二次操作,舍掉
当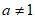 时,
时,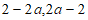 至少有一个为负数,
至少有一个为负数,
所以此时必须有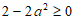 ,即
,即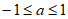 ,所以
,所以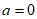 或
或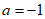
经检验,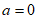 或
或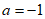 符合要求
符合要求
综上: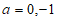
(Ⅲ)能经过有限次操作以后,使得得到的数表所有的行和与所有的列和均为非负实数。证明如下:
记数表中第i行第j列的实数为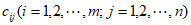 ,各行的数字之和分别为
,各行的数字之和分别为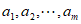 ,各列的数字之和分别为
,各列的数字之和分别为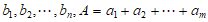 ,
,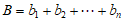 ,数表中
,数表中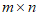 个实数之和为S,则
个实数之和为S,则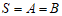 ,记
,记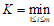
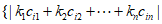
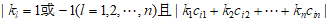
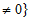
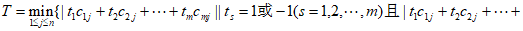
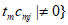
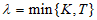 。
。
按要求操作一次时,使该行的行和(或该列的列和)由负变正,都会引起A(和B)增大,从而也就使得S增加,增加的数值大于等于2λ,但是每次操作都只是改变数表中某行(或某列)各数的符号,而不改变其绝对值,故S必然不超过最初的数表中m×n个实数的绝对值之和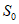 ,于是操作次数N必须满足
,于是操作次数N必须满足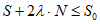 ,故最多不超过
,故最多不超过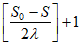 次操作。
次操作。