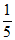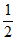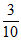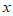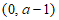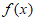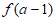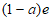本试卷满分共150分,作答时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合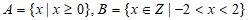 ,那么
,那么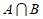 =
=
A. {0,1} B. 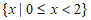 C.
C. 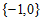 D.
D.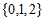
2. 在等差数列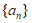 中,若
中,若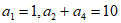 ,则
,则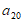 =
=
A. 35 B. 37 C. 39 D. 41
3. 某几何体的三视图如图所示,则该几何体的表面积等于
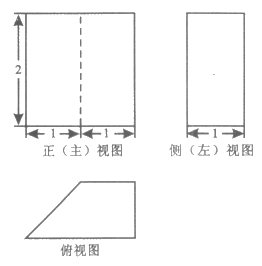
A. 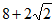 B.
B. 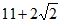 C.
C. 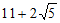 D.
D.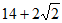
4. 若函数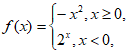 则函数
则函数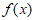 的值域为
的值域为
A. 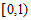 B.
B. 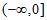 C.
C. 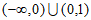 D.
D.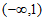
5. 若关于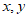 的方程组
的方程组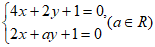 无解,则a=
无解,则a=
A. 2 B. 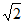 C. 1 D.
C. 1 D.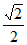
6. 下列函数中,同时满足①对于定义域内的任意x,都有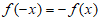 ;②存在区间D,
;②存在区间D,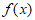 在区间D上单调递减的函数是
在区间D上单调递减的函数是
A. 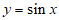 B.
B. 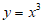 C.
C. 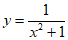 D.
D.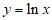
7. 已知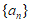 是等比数列,
是等比数列,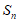 为其前n项和,那么”
为其前n项和,那么”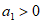 “是”数列
“是”数列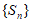 为递增数列”的
为递增数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 某校实行选科走班制度(语文、数学、英语为必选科目,此外学生需在物理、化学、生物、历史、地理、政治六科中任选三科),根据学生选科情况,该校计划利用三天请专家对九个学科分别进行学法指导,每天依次安排三节课,每节课一个学科,语文、数学、英语只排在第二节;物理、政治排在同一天,化学、地理排在同一天,生物、历史排在同一天,则不同的排课方案的种数为
A. 36 B. 48 C. 144 D. 288
9. 在平面直角坐标系中,A,B是直线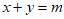 上的两点,且
上的两点,且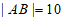 ,若对于任意点
,若对于任意点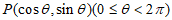 ,存在A,B使∠APB=90°成立,则m的最大值为
,存在A,B使∠APB=90°成立,则m的最大值为
A. 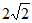 B. 4 C.
B. 4 C. 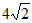 D. 8
D. 8
10. 为了预防某种病毒,某商场需要通过喷洒药物对内部空间进行全面消毒,出于对顾客身体健康的考虑,相关部门规定空气中这种药物的浓度不超过0.25毫克/立方米时,顾客方可进入商场。已知从喷洒药物开始,商场内部的药物浓度y(毫克/立方米)与时间t(分钟)之间的函数关系为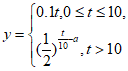 (a为常数),函数图象如图所示,如果商场规定10:00顾客可以进入商场,那么开始喷洒药物的时间最迟是
(a为常数),函数图象如图所示,如果商场规定10:00顾客可以进入商场,那么开始喷洒药物的时间最迟是
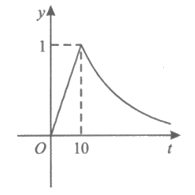
A. 9:40 B. 9:30 C. 9:20 D. 9:10
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 在复平面内,复数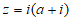 对应的点在直线
对应的点在直线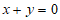 上,则实数a=_________。
上,则实数a=_________。
12. 已知双曲线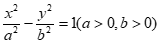 的一条渐近线方程为
的一条渐近线方程为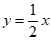 ,那么该双曲线的离心率为_____________。
,那么该双曲线的离心率为_____________。
13. 已知正六边形ABCDEF的边长为1,那么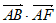 =__________;若
=__________;若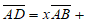
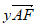 ,则
,则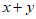 =__________。
=__________。
14. 函数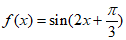 的最小正周期T=__________,将函数
的最小正周期T=__________,将函数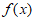 的图象向左平移
的图象向左平移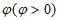 个单位长度,得到函数
个单位长度,得到函数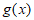 的图象,若函数
的图象,若函数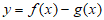 的最大值为2,则
的最大值为2,则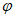 的值可以为_____________。
的值可以为_____________。
15. 对于平面直角坐标系内的任意两点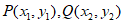 ,定义它们之间的一种”距离”为
,定义它们之间的一种”距离”为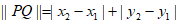 。已知不同三点
。已知不同三点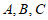 满足
满足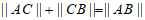 ,给出下列四个结论:
,给出下列四个结论:
①A,B,C三点可能共线;
②A,B,C三点可能构成锐角三角形;
③A,B,C三点可能构成直角三角形;
④A,B,C三点可能构成钝角三角形。
其中所有正确结论的序号是_____________。
三、解答题:共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
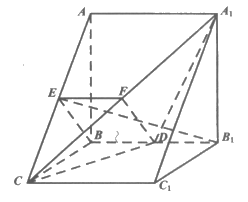
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1和BCC1B1都是正方形,平面ABB1A1⊥平面BCC1B1,D,E分别为BB1,AC的中点。
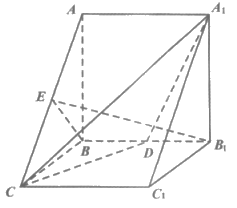
(Ⅰ)求证:BE∥平面A1CD;
(Ⅱ)求直线B1E与平面A1CD所成角的正弦值。
17.(本小题13分)
在△ABC中,已知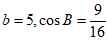 ,再从条件①、条件②这两个条件中选择一个作为已知。
,再从条件①、条件②这两个条件中选择一个作为已知。
(Ⅰ)求sin A;
(Ⅱ)求△ABC的面积。
条件①: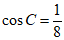 ;条件②:
;条件②: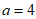 。
。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
18. (本小题14分)
全社会厉行勤俭节约,反对餐饮浪费,某市为了解居民外出就餐有剩余时是否打包,进行了一项”舌尖上的浪费”的调查,对该市的居民进行简单随机抽样,将获得的数据按不同年龄段整理如下表:
男性 | 女性 | |||
打包 | 不打包 | 打包 | 不打包 | |
第1段 | 250 | 650 | 450 | 650 |
第2段 | 300 | 600 | 550 | 550 |
第3段 | 600 | 400 | 750 | 250 |
第4段 | 850 | 350 | 650 | 150 |
假设所有居民外出就餐有剩余时是否打包相互独立。
(Ⅰ)分别估计该市男性居民外出就餐有剩余时打包的概率,该市女性居民外出就餐有剩余时打包的概率;
(Ⅱ)从该市男性居民中随机抽取1人,女性居民中随机抽取1人,记这2人中恰有X人外出就餐有剩余时打包,求X的分布列;
(Ⅲ)假设每年龄段居民外出就餐有剩余时打包的概率与表格中该段居民外出就餐有剩余时打包的频率相等,用”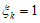 “表示第k段居民外出就餐有剩余时打包,”
“表示第k段居民外出就餐有剩余时打包,”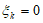 “表示第k段居民外出就餐有剩余时不打包(
“表示第k段居民外出就餐有剩余时不打包(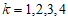 ),写出方差
),写出方差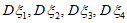 的大小关系。(只需写出结论)
的大小关系。(只需写出结论)
19.(本小题15分)
已知函数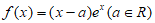 。
。
(Ⅰ)当a=1时,求曲线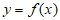 在点
在点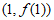 处的切线方程;
处的切线方程;
(Ⅱ)如果函数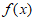 在区间(0,1)上有极值,且
在区间(0,1)上有极值,且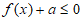 对于
对于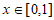 恒成立,求a的取值范围。
恒成立,求a的取值范围。
20.(本小题15分)
已知椭圆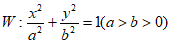 过
过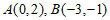 两点。
两点。
(Ⅰ)求椭圆W的方程;
(Ⅱ)直线AB与x轴交于点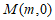 ,过点M作不垂直于坐标轴且与AB不重合的直线
,过点M作不垂直于坐标轴且与AB不重合的直线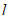 ,
,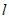 与椭圆W交于C,D两点,直线
与椭圆W交于C,D两点,直线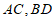 分别交直线
分别交直线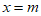 于P,Q两点,求证:
于P,Q两点,求证: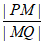 为定值。
为定值。
21. (本小题15分)
已知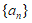 是由正整数组成的无穷数列,该数列前n项的最大值记为
是由正整数组成的无穷数列,该数列前n项的最大值记为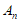 ,最小值记为
,最小值记为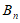 ,令
,令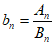 。
。
(Ⅰ)若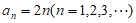 ,写出
,写出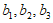 的值;
的值;
(Ⅱ)证明: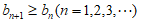 ;
;
(Ⅲ)若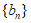 是等比数列,证明:存在正整数
是等比数列,证明:存在正整数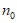 ,当
,当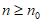 时,
时,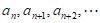 是等比数列。
是等比数列。
【试题答案】
一、选择题(共10小题,每小题4分,共40分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | C | B | D | C | A | B | D | C | B |
二、填空题(共5小题,每小题5分,共25分)
11. 1 12. 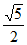 13.
13. 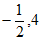 14.
14. 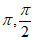 (答案不唯一)
(答案不唯一)
15.①③④(全部选对得5分,不选或有错选得0分,其他得3分)
三、解答题(共6小题,共85分)
16. (本小题13分)
(Ⅰ)证明:取A1C中点F,连接DF,EF,
在△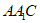 中,E,F分别是
中,E,F分别是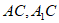 的中点,
的中点,
所以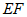 ∥
∥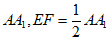 ,
,
在三棱柱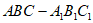 中,
中,
四边形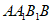 为正方形,D为
为正方形,D为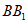 中点,
中点,
所以BD∥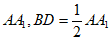 ,
,
所以BD∥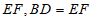 ,
,
所以四边形BEFD为平行四边形,
所以BE∥DF。 2分
因为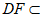 平面
平面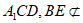 平面
平面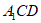 ,
,
所以BE∥平面A1CD。 5分
(Ⅱ)解:因为平面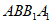 ⊥平面
⊥平面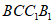 ,平面
,平面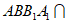 平面
平面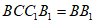 ,
,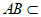 平面
平面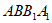 ,
,
正方形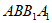 中AB⊥BB1,
中AB⊥BB1,
所以AB⊥平面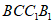 ,
,
所以AB⊥BC,
正方形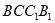 中BC⊥BB1。
中BC⊥BB1。
如图建立平面直角坐标系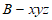 。 7分
。 7分
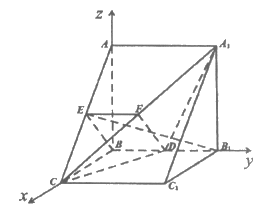
不妨设AB=BC=BB1=2,则B(0,0,0),A(0,0,2),C(2,0,0),B1(0,2,0),A1(0,2,2),D(0,1,0),E(1,0,1)。
所以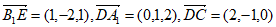 。 9分
。 9分
设平面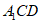 的法向量
的法向量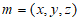 ,则
,则
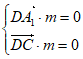 ,即
,即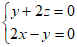 。
。
令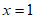 ,则
,则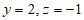 。
。
于是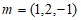 。 11分
。 11分
设直线B1E与平面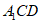 所成的角为
所成的角为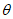 ,
,
所以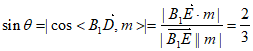 ,
,
所以直线B1E与平面A1CD所成角的正弦值为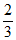 。 13分
。 13分
17.(本小题13分)
解①:(Ⅰ)因为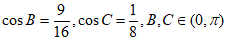 ,
,
所以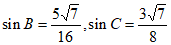 , 4分
, 4分
所以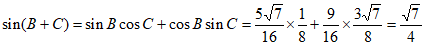 , 6分
, 6分
所以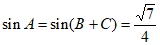 。 7分
。 7分
(Ⅱ)由正弦定理得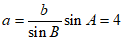 , 10分
, 10分
所以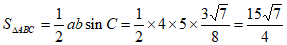 。 13分
。 13分
解②:(Ⅰ)由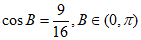 得
得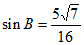 , 3分
, 3分
由正弦定理得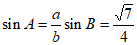 。 7分
。 7分
(Ⅱ)由余弦定理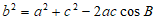 ,得
,得
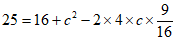 ,
,
即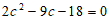 ,
,
解得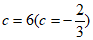 舍, 10分
舍, 10分
所以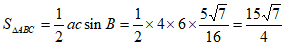 。 13分
。 13分
18. (本小题14分)
(Ⅰ)解:设该市男性居民外出就餐有剩余时打包为事件A;设该市女性居民外出就餐有剩余时打包为事件B。
男性居民外出就餐有剩余时打包的有250+300+600+850=2000人,男性居民外出就餐有剩余时不打包的有650+600+400+350=2000人,被调查的男性居民有2000+2000=4000人,
所以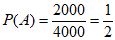 。 3分
。 3分
女性居民外出就餐有剩余时打包的有450+550+750+650=2400人,女性居民外出就餐有剩余时不打包的有650+550+250+150=1600人,被调查的女性居民有2400+1600=4000人,
所以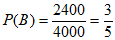 。 5分
。 5分
(Ⅱ)解:X的所有可能取值为0,1,2。 6分
由题设知,事件A与B相互独立,且
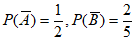 , 8分
, 8分
所以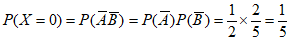 ,
,
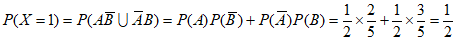 ,
,
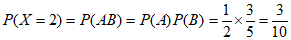 。 11分
。 11分
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
12分
(Ⅲ)解: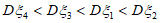 14分
14分
19.(本小题15分)
解:(Ⅰ)当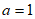 时,因为
时,因为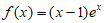 ,
,
所以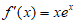 。 1分
。 1分
因为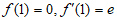 , 3分
, 3分
所以曲线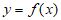 在点
在点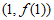 处的切线方程为
处的切线方程为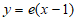 ,
,
即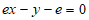 。 5分
。 5分
(Ⅱ)因为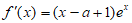 ,函数
,函数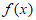 在区间
在区间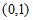 上有极值,
上有极值,
所以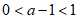 ,
,
所以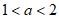 。 8分
。 8分
当x变化时,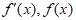 的变化情况如下表:
的变化情况如下表:
| 0 |
|
|
| 1 |
| - | 0 | + | ||
| -a | ↘ |
| ↗ |
|
11分
因为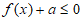 对于
对于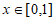 恒成立,
恒成立,
所以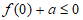 ,且
,且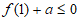 , 13分
, 13分
所以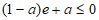 ,即
,即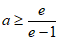 ,
,
因为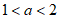 ,
,
所以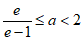 。 15分
。 15分
20.(本小题15分)
解:(Ⅰ)由椭圆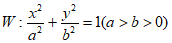 过
过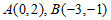 两点,得
两点,得
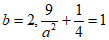 , 2分
, 2分
所以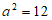 , 3分
, 3分
所以椭圆W的方程为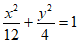 。 4分
。 4分
(Ⅱ)由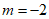 ,
,
设直线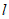 的方程为
的方程为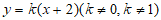 。 6分
。 6分
由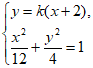 得
得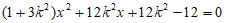 ,
,
且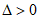 。
。
设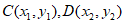 ,则
,则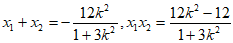 , 8分
, 8分
记直线AC的方程为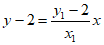 ,
,
令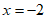 ,得P点的纵坐标
,得P点的纵坐标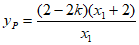 , 10分
, 10分
记直线BD的方程为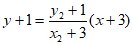 ,
,
令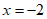 ,得Q点的纵坐标
,得Q点的纵坐标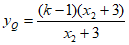 。 12分
。 12分
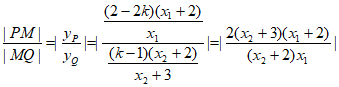
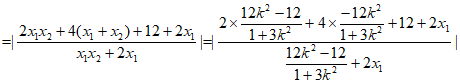
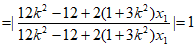 。
。
所以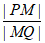 为定值1。 15分
为定值1。 15分
方法2:
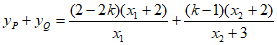
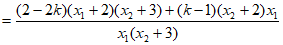
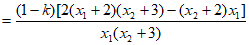
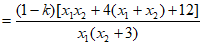
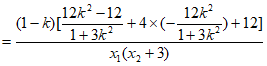
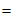
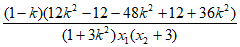
=0。
所以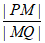 为定值1。 15分
为定值1。 15分
21.(本小题15分)
解:(Ⅰ)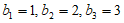 。 3分
。 3分
(Ⅱ)由题意知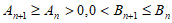 , 5分
, 5分
所以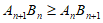 ,
,
所以
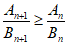 ,即
,即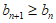 。 7分
。 7分
(Ⅲ)由题意知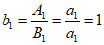 ,及
,及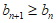 , 8分
, 8分
①当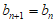 时,得
时,得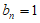 ,即
,即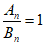 ,
,
所以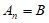 ,
,
所以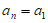 ,
,
即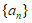 为公比等于1的等比数列。 10分
为公比等于1的等比数列。 10分
②当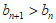 时,令
时,令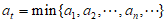 ,则
,则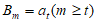 。 11分
。 11分
当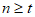 时,
时,
显然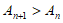 ,
,
若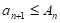 ,则
,则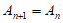 ,与
,与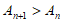 矛盾,
矛盾,
所以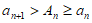 ,即
,即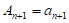 。 13分
。 13分
取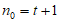 ,当
,当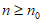 时,
时,
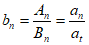 ,显然
,显然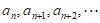 是等比数列。
是等比数列。
综上,存在正整数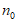 ,使得
,使得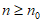 时,
时,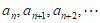 是等比数列。 15分
是等比数列。 15分
(若用其他方法解题,请酌情给分)