北京市西城区2020-2021学年下学期高一年级期末考试数学试卷
本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设向量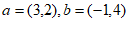 ,则
,则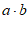 =
=
A. 11 B. 9 C. 7 D. 5
2. sin330°=
A. 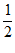 B.
B. 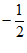 C.
C. 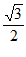 D.
D. 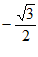
3. 在复平面内,复数z对应的点Z如图所示,则复数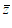 =
=
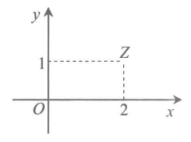
A. 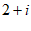 B.
B. 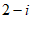 C.
C. 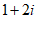 D.
D. 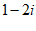
4. 某圆锥的母线长为5cm,底面半径长为3cm,则该圆锥的体积为
A. 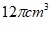 B.
B. 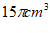 C.
C. 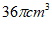 D.
D. 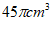
5. 函数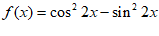 的最小正周期是
的最小正周期是
A. 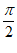 B.
B. 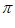 C.
C. 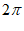 D.
D. 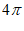
6. 若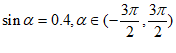 ,则符合条件的角
,则符合条件的角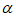 有
有
A. 1个 B. 2个 C. 3个 D. 4个
7. 函数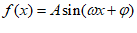 (其中
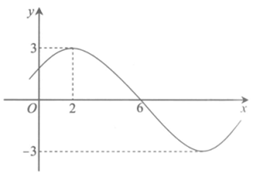
(其中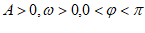 )的图象的一部分如图所示,则此函数的解析式是
)的图象的一部分如图所示,则此函数的解析式是
A. 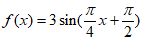 B.
B. 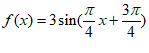
C. 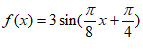 D.
D. 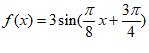
8. 向量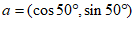 与
与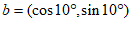 的夹角为
的夹角为
A. 30° B. 40° C. 60° D. 90°
9. 在△ABC中,角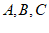 所对的边分别为
所对的边分别为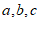 ,则”
,则”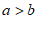 “是”
“是”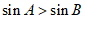 “的
“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10. 已知单位向量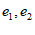 满足
满足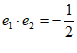 ,若非零向量
,若非零向量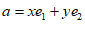 ,其中
,其中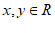 ,则
,则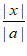 的最大值为
的最大值为
A. 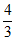 B.
B. 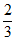 C.
C. 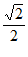 D.
D. 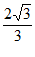
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 设复数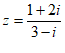 ,则
,则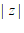 =_________。
=_________。
12. 已知半径为r的球的表面积为36πcm2,那么半径为2r的球的表面积为__________cm2。
13. 在锐角△ABC中,角A,B,C所对的边分别为a,b,c。若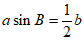 ,则A=_________。
,则A=_________。
14. 已知向量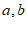 满足
满足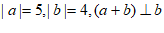 ,那么
,那么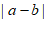 =__________。
=__________。
15. 设函数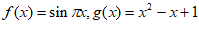 ,有以下四个结论:
,有以下四个结论:
①函数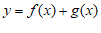 是周期函数;
是周期函数;
②函数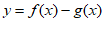 的图象是轴对称图形;
的图象是轴对称图形;
③函数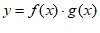 的图象关于坐标原点对称;
的图象关于坐标原点对称;
④函数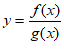 存在最大值。
存在最大值。
其中,所有正确结论的序号是____________。
三、解答题:共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
已知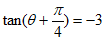 。
。
(Ⅰ)求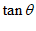 的值;
的值;
(Ⅱ)求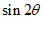 的值。
的值。
17. (本小题14分)
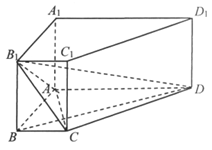
如图,在四棱柱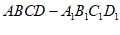 中,
中,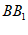 ⊥平面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,且
⊥平面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,且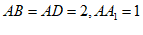 。
。
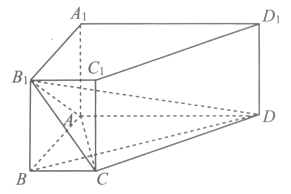
(Ⅰ)求三棱锥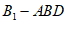 的体积;
的体积;
(Ⅱ)求证:BC∥平面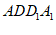 ;
;
(Ⅲ)求证: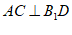 。
。
18. (本小题13分)
在△ABC中,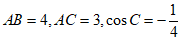 。
。
(Ⅰ)求△ABC的面积;
(Ⅱ)求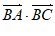 的值。
的值。
19. (本小题15分)
已知函数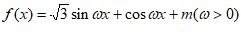 同时满足下列三个条件中的二个:
同时满足下列三个条件中的二个:
①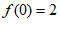 ; ②最大值为2;
; ②最大值为2;
③最小正周期为π。
(Ⅰ)求出所有可能的函数f(x),并说明理由;
(Ⅱ)从符合题意的函数中选择一个,求其单调增区间。
20. (本小题15分)
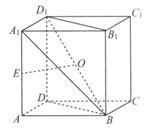
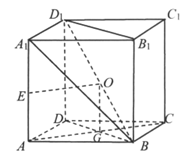
如图,在正方体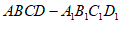 中,
中,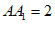 ,E为
,E为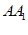 的中点,O为
的中点,O为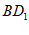 的中点。
的中点。
(Ⅰ)求证:平面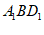 ⊥平面
⊥平面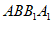 ;
;
(Ⅱ)求证:EO⊥平面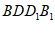 ;
;
(Ⅲ)设P为正方体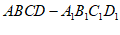 棱上一点,给出满足条件
棱上一点,给出满足条件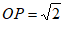 的点P的个数。(结论不要求证明)
的点P的个数。(结论不要求证明)
21. (本小题15分)
设函数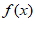 的定义域为R,若存在常数T,
的定义域为R,若存在常数T,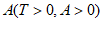 ,使得对于任意
,使得对于任意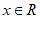 ,
,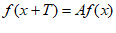 成立,则称函数
成立,则称函数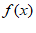 具有性质P。
具有性质P。
(Ⅰ)判断函数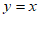 和
和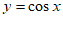 具有性质P?(结论不要求证明)
具有性质P?(结论不要求证明)
(Ⅱ)若函数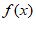 具有性质P,且其对应的
具有性质P,且其对应的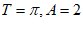 。已知当
。已知当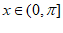 时,
时,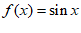 ,求函数
,求函数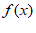 在区间
在区间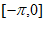 上的最大值;
上的最大值;
(Ⅲ)若函数g(x)具有性质P,且直线x=m为其图像的一条对称轴,证明:g(x)为周期函数。
【试题答案】
一、选择题:本大题共10小题,每小题4分,共40分。
1. D 2. B 3. B 4. A 5. A
6. C 7. C 8. B 9. C 10. D
二、填空题:本大题共5小题,每小题5分,共25分。
11. 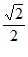 12.
12. 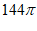 13.
13. 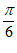 14.
14. 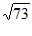 15. ②④
15. ②④
注:第15题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题:本大题共6小题,共85分。其他正确解答过程,请参照评分标准给分。
16. (本小题13分)
解:(Ⅰ)由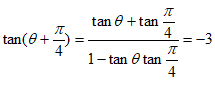 , 3分
, 3分
解得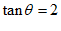 。 5分
。 5分
(Ⅱ)由(Ⅰ),得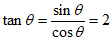 ,① 6分
,① 6分
又因为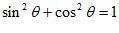 , ② 8分
, ② 8分
联立①②,解得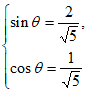
或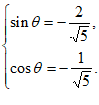 11分
11分
所以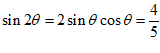 。 13分
。 13分
17. (本小题14分)
(Ⅰ)解:因为在四棱柱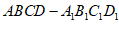 中,BB1⊥平面
中,BB1⊥平面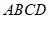 ,∠BAD=90°,
,∠BAD=90°,
所以三棱锥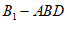 的体积
的体积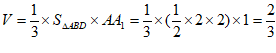 。 3分
。 3分
(Ⅱ)证明:因为AD∥BC,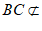 平面
平面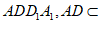 平面
平面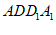 ,
,
所以BC∥平面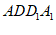 。 6分
。 6分
(Ⅲ)证明:因为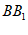 ⊥平面ABCD,AC
⊥平面ABCD,AC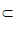 平面ABCD,
平面ABCD,
所以BB1⊥AC。 8分
又因为AC⊥BD,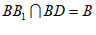 ,
,
所以AC⊥平面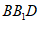 , 11分
, 11分
又因为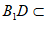 平面
平面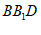 ,
,
所以AC⊥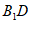 。 14分
。 14分
18. (本小题13分)
解:(Ⅰ)由余弦定理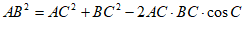 , 3分
, 3分
得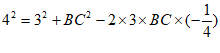 ,
,
解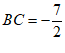 (舍)或
(舍)或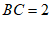 , 5分
, 5分
由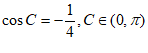 ,得
,得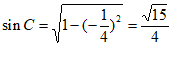 。 7分
。 7分
所以△ABC的面积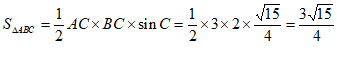 。 9分
。 9分
(Ⅱ)由余弦定理,得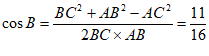 , 11分
, 11分
所以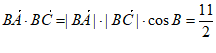 。 13分
。 13分
19. (本小题15分)
解:(Ⅰ)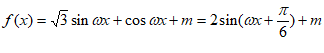 , 3分
, 3分
若函数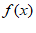 满足条件①②:
满足条件①②:
由条件①: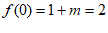 ,得
,得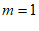 ,即
,即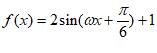 ,
,
所以当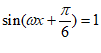 时,
时,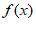 有最大值3,
有最大值3,
这与②矛盾。即函数f(x)不能同时满足条件①②。 5分
若函数f(x)满足条件①③:
由条件①,得m=1。
由条件③,得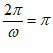 ,解得
,解得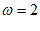 ,
,
所以此时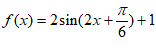 , 7分
, 7分
若函数f(x)满足条件②③:
又因为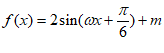 ,
,
所以当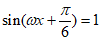 时,
时,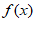 的最大值
的最大值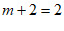 ,
,
解得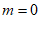 。
。
由条件③,得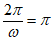 ,解得
,解得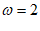 ,
,
所以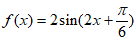 。 9分
。 9分
综上,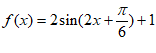 或
或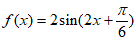 。
。
(Ⅱ)不妨选择函数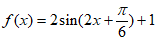 ,
,
由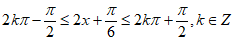 , 11分
, 11分
得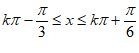 , 13分
, 13分
所以函数f(x)的单调增区间为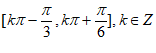 。 15分
。 15分
(注:单调区间写成开区间亦可。)
20. (本小题15分)
(Ⅰ)证明:在正方体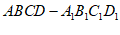 中,
中,
因为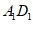 ⊥平面
⊥平面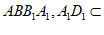 平面
平面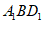 ,
,
所以平面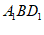 ⊥平面
⊥平面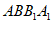 。 4分
。 4分
(Ⅱ)证明:连接AC,设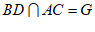 ,连接OG,
,连接OG,
因为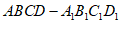 为正方体,
为正方体,
所以AE∥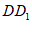 ,且
,且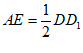 ,且G是BD的中点,
,且G是BD的中点,
又因为O是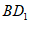 的中点,
的中点,
所以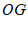 ∥
∥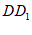 ,且
,且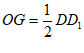 ,
,
所以OG∥AE,且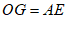 ,
,
即四边形AGOE是平行四边形,
所以EO∥AG。 6分
由正方体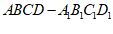 ,得
,得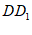 ⊥平面ABCD,AG⊥BD,
⊥平面ABCD,AG⊥BD,
所以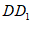 ⊥AG,
⊥AG,
又因为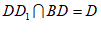 ,
,
所以AG⊥平面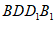 , 9分
, 9分
所以EO⊥平面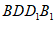 。 11分
。 11分
(Ⅲ)解:满足条件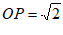 的点P有12个。 15分
的点P有12个。 15分
21. (本小题15分)
解:(Ⅰ)函数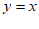 不具有性质P;函数
不具有性质P;函数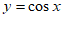 具有性质P。 3分
具有性质P。 3分
(Ⅱ)设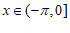 ,则
,则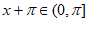 , 4分
, 4分
由题意,得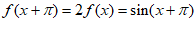 ,
,
所以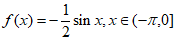 。 6分
。 6分
由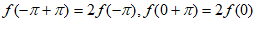 ,得
,得 ,
,
所以当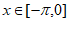 时,
时,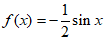 , 7分
, 7分
故当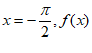 在区间
在区间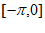 上有最大值
上有最大值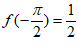 。 9分
。 9分
(Ⅲ)当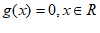 时,结论显然成立; 10分
时,结论显然成立; 10分
以下考虑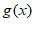 不恒等于0的情况,即
不恒等于0的情况,即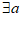 ,使得
,使得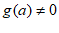 ,
,
由直线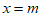 为函数
为函数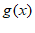 图象的一条对称轴,得
图象的一条对称轴,得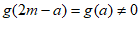 , 12分
, 12分
由题意,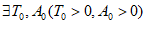 ,使得
,使得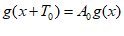 成立,
成立,
所以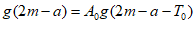 ,即
,即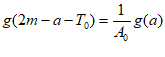 。
。
由直线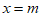 为函数
为函数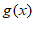 图象的一条对称轴,得
图象的一条对称轴,得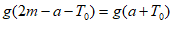 。
。
又因为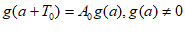 ,
,
所以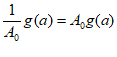 ,即
,即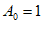 ,
,
故对于任意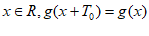 成立,其中
成立,其中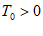 ,
,
综上,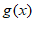 为周期函数。 15分
为周期函数。 15分
