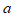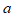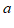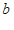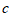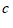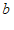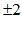北京101中学2020-2021学年下学期初中七年级期末考试数学试卷
一、选择题:本大题共8小题,共24分。
1. 在实数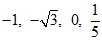 中,最小的实数是(
中,最小的实数是(
)
A. 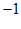 B.
B. 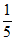 C.
C. 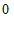 D.
D. 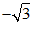
2. 二元一次方程
的解是(
)
A. B. C. D.
3. 皮影戏是中国民间古老的传统艺术,2011年中国皮影戏入选人类非物质文化遗产代表作名录. 图1是孙悟空的皮影造型,在下面右侧的四个图中,能由图1经过平移得到的是(
)
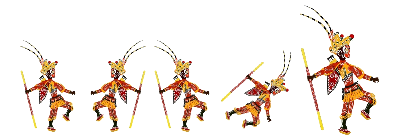
图1 A B C D
4. 如图,直线a,b相交于点O,如果∠1+∠2=100°,那么∠3是( )
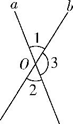
A. 50° B. 100° C. 130° D. 150°
5. 已知实数a、b,若a>b,则下列结论正确的是(
)
A. 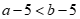 B.
B. 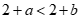
C. 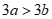 D.
D. 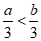
6. 下列调查中,适宜采用全面调查方式的是(
)
A. 调查某中学初一年级三班学生视力情况
B. 调查我市居民对“垃圾分类“有关内容的了解程度
C. 调查某批次汽车的抗撞击能力
D. 了解一批手机电池的使用寿命
7. 一个容量为80的样本中,最大数是141,最小数是50,取组距为10,可以分成(
)组
A. 10组 B. 9组 C. 8组 D. 7组
8. 某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告。15秒的广告每播一次收费0.6万元,30秒的广告每播一次收费1万元. 若要求每种广告播放不少于2次,则电视台在播放时收益最大的播放方式是(
)
A. 15秒的广告播放2次,30秒的广告播放4次
B. 15秒的广告播放4次,30秒的广告播放2次
C. 15秒的广告播放2次,30秒的广告播放3次
D. 15秒的广告播放3次,30秒的广告播放2次
二、填空题:本大题共8小题,共24分。
9. 若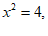
则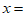
。
10. 如果
是二元一次方程
的解,那么m的值为
。
11. 不等式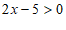 的最小整数解是
的最小整数解是
。
12. 为了了解某校800名初一学生的睡眠时间,从中抽取80名学生进行调查,在这个问题中,样本容量是
。
13. 已知点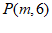 在第二象限内,则m的值可以是(写出一个即可)
在第二象限内,则m的值可以是(写出一个即可)
。
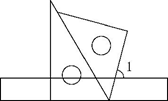
14. 将一副三角板和一个直尺按如图所示的位置摆放,则∠1的度数为
。
15. 某商店今年1~4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2。
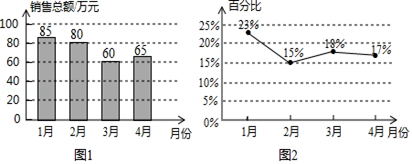
有以下五个结论:
①
从1月到4月,手机销售总额连续下降;
②
从1月到4月,音乐手机销售额在当月手机销售总额中的占比连续下降;
③
音乐手机4月份的销售额比3月份有所上升;
④ 1~4月中,音乐手机销售额最低的是3月;
⑤ 1~4月音乐手机的销售额一共53.4万元。
其中正确的结论有
(填写序号)。
16. 为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初一(9)班举办了“古诗词“大赛。现有小恩、小地、小奕三位同学进入了最后冠军的角逐,决赛共分为六轮,规定:每轮分别决出第1,2,3名(没有并列),对应名次的得分都分别为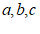 (
(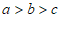 且
且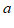 ,
,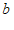 ,
,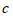 均为正整数)。选手最后得分为各轮得分之和,得分最高者为冠军。下表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,小奕同学第三轮的得分为
均为正整数)。选手最后得分为各轮得分之和,得分最高者为冠军。下表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,小奕同学第三轮的得分为
分。
第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 | 第六轮 | 最后得分 | |
小恩 |
|
| 27 | ||||
小地 |
|
|
| 11 | |||
小奕 |
|
| 10 |
三、解答题:本大题共12小题,共52分。其中17-25题每题4分,26-27题每题5分,28题6分。
17. 计算: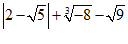 。
。
18. 解方程组:
。
19. 解不等式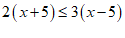 ,并在数轴上把解集表示出来。
,并在数轴上把解集表示出来。
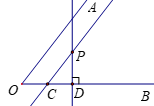
20. 已知:∠AOB及∠AOB内部一点P。
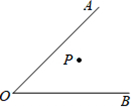
(1)过点P作直线PD⊥OB于点D;
(2)过点P
作直线PC∥OA交OB于点C;
(3)∠AOB与∠CPD的数量关系是
。
21. 如图,在平面直角坐标系xOy中,A,B两点的坐标分别为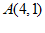 ,
,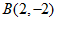 。
。
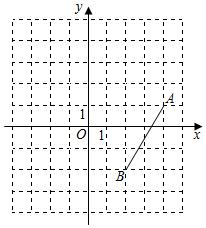
(1)过点B作x轴的垂线,垂足为M,在BM的延长线上截取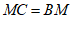 ,平移线段AB,使点A移动到点C,画出平移后的线段CD;
,平移线段AB,使点A移动到点C,画出平移后的线段CD;
(2)直接写出C,D两点的坐标;
;
(3)直接写出 的面积:
的面积:
。
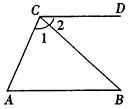
22. 如图,AB∥CD,∠A=70°,∠2=35°,求∠1的度数。
23. 新修订的《北京市生活垃圾管理条例》于2020年5月1日正式施行。新修订的分类标准将生活垃圾分为厨余垃圾、有害垃圾、其他垃圾和可回收物四类,为了促使居民更好地了解垃圾分类知识,小明所在的小区随机抽取了50名居民进行线上垃圾分类知识测试。将参加测试的居民的成绩进行收集、整理,绘制成如图所示的频数分布表和频数分布直方图:
a. 线上垃圾分类知识测试频数分布表:
成绩分组 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
频数 | 3 | 9 | m | 12 | 8 |
b. 线上垃圾分类知识测试频数分布直方图:
c. 成绩在80≤x<90这一组的成绩为:
80,81,82,83,83,85,86,86,87,88,88,89
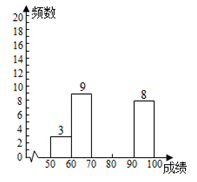
根据以上信息,回答下列问题:
(1)表中m的值为
;
(2)请补全频数分布直方图;
(3)小明居住的社区大约有居民2000人,若达到测试成绩85分为优秀,那么估计小明所在的社区优秀的人数约为
人。
24. 为了更好的开展“我爱阅读“活动,小明针对某校七年级学生(共16个班,610名学生)课外阅读喜欢图书的种类(每人只能选一种书籍)进行了调查。
(1)小明采取的下列调查方式中,比较合理的是
;
A. 对七年级(1)班的全体同学进行问卷调查;
B. 对七年级各班的语文科代表进行问卷调查;
C. 对七年级各班学号为3的倍数的所有同学进行问卷调查。
(2)小明根据问卷调查的结果绘制了如下两幅不完整的统计图,根据图中提供的信息解答下列问题:
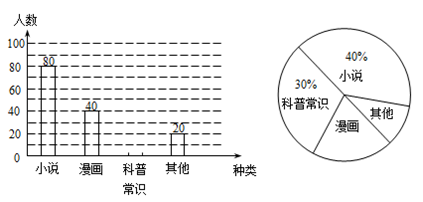
①本次抽样调查的样本容量为
;
②补全条形统计图;
③在扇形统计图中,“其他“所在的扇形的圆心角等于
度。
25. 已知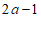 的平方根是
的平方根是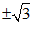 ,
,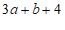 的立方根是
的立方根是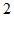 ,求
,求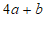 的算术平方根。
的算术平方根。
26. 某公司后勤部准备去超市采购牛奶和咖啡若干箱,现有两种不同的购买方案,如下表:
牛奶(箱 | 咖啡(箱 | 金额(元 | |
方案一 | 20 | 10 | 1100 |
方案二 | 10 | 20 | 1300 |
(1)求牛奶与咖啡每箱分别为多少元?
(2)超市中该款咖啡和牛奶有部分因保质期临近,进行打六折的促销活动,后勤部根据需要选择原价或打折的咖啡和牛奶,此次采购共花费了1800元,其中购买打折的牛奶箱数是所有牛奶、咖啡的总箱数的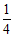 ,则此次按原价采购的咖啡有
,则此次按原价采购的咖啡有
箱。(直接写出答案)
27. 阅读下列材料:
问题:已知,且,,试确定的取值范围。
解:∵,∴,
又∵,∴,
∴,
又∵
,
∴
①
∴
,
即
②
①+②得
,
∴的取值范围是。
请按照上述方法,完成下列问题:
(1)已知,且,,则的取值范围是
;
的取值范围是
;
(2)已知,且,,若根据上述做法得到的取值范围是,求a、b的值。
28. 在平面直角坐标系xOy中,A1,A2,…,Ak是k个互不相同的点,若这k个点横坐标的不同取值有m个,纵坐标的不同取值有n个,p =m+n,则称p为这k个点的“平面特征值“,记为T<A1,A2,…,Ak> = p. 如:点M(2,1),点N(3,1),则T<M,N> =2+1=3。
如图,正方形ABCD的边AB在x轴上,CD交y轴于点E,已知O为AB的中点,点B的坐标为(4,0),
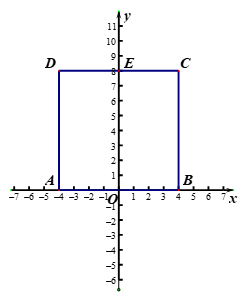
(1)T<A,B> =
,T<A,B,E > =
;
(2)点F(0,b)为y轴上一动点,过点P作直线l∥x轴,直线l与直线AC,直线BD的交点记为P,Q,请直接写出T<A,B,C,D,E,F,P,Q >的所有可能的取值,以及相应的b的取值范围。
参考答案
一、选择题:本大题共8小题,每题3分,共24分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | D | B | C | C | A | A | B |
二、填空题:本大题共8小题,每题3分,共24分.
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 3 | 3 | 80 | 答案不唯一,如:-1 | 75 | ③,④,⑤ | 2 |
16.【提示】
由题可知:(a+b+c)×6=27+11+10=48,其中a>b>c且a,b,c均为正整数。
∴a+b+c也是正整数,
∴a+b+c=8。
若每轮比赛第一名得分a为4,则甲最后得分最高为:4×6=24<27,
∴a>4,
∵又a>b>c,b+c最小取3,
∴4<a<6。
∴a=5,b=2,c=1,
∴每轮比赛第一名得分a为5,
小恩5轮得第一,1轮得第三;
小地4轮得第三,1轮得第一,1轮得第二;
小奕4轮得第二,2轮得第三。
∴小恩第三轮得5分,小地第三轮得1分,小奕第三轮得2分。
三、解答题:共52分.
17. (4分)原式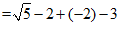 —————3分
—————3分
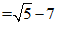 。
。
–4分
18. (4分)
【解答】解: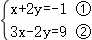 ,
,
①+②,得:4x=8,—–1分
解得x=2,————-2分
将x=2代入①,得:2+2y=﹣1,
解得y=﹣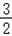 ,————-3分
,————-3分
∴方程组的解为. –4分
19. (4分)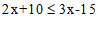 —1分
—1分
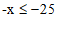 —————————2分
—————————2分
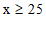 —–3分
—–3分
解集在数轴上表示正确————–4分
20. (4分)解:(1)、(2)如图;———————3分
(直角符号占一分,两条直线各占1分,直线画成射线或线段的酌情扣分)
(3)结论:∠AOB+∠CPD=90°. (或∠AOB与∠CPD互余)———————4分
21. (4分)(1)如图;————-2分
(直角符号不占分,其他有错酌情扣分)
(2)C(2,2),D(0,-1);—3分
(有错不给分)
(3)4————4分
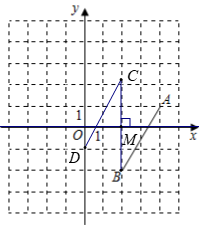
22. (4分)∵CD∥AB,∠A=70°,
∴∠ACD =180°-∠A=110°,————2分
∵∠2=35°,
∴∠1 =∠ACD–∠2=75°。
———–4分
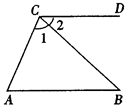
方法2:先由“两直线平行,内错角相等“求出∠B=35°,—————2分
再根据三角形内角和定理求出∠1=75°。
———–4分
23. (4分)(1)18;—1分
(2)图略;———–3分
(3)600;————4分
24. (4分)
(1)C————-1分
(2)①200;②60略;③36——-4分
25. (4分)根据题意可得: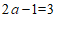 ,
,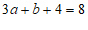 ,———–2分
,———–2分
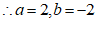 ,———–3分
,———–3分
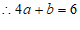 ,
,
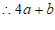 的算术平方根是
的算术平方根是 . ———–4分
. ———–4分
26. (5分)
解:(1)设牛奶一箱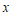 元,咖啡一箱
元,咖啡一箱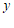 元,
元,
由题意得: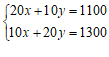 ,———–2分(列对一个方程给1分,没有设未知数扣1分)
,———–2分(列对一个方程给1分,没有设未知数扣1分)
解得: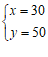 ,———-3分
,———-3分
答:牛奶与咖啡每箱分别为30元、50元;(没有写答不扣分)
(2)9. ———–5分
(如果写9,36,63,给1分;写9,36,给1分;写9,给2分;其他写法给0分)
【提示】设牛奶与咖啡总箱数为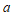 ,则打折的牛奶箱数为
,则打折的牛奶箱数为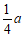 ,
,
打折牛奶价格为: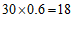 (元
(元 ,打折咖啡价格为:
,打折咖啡价格为: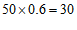 (元
(元 ,
,
即打折咖啡价格与牛奶原价相同,
设原价咖啡为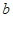 箱,则打折咖啡与原价牛奶共有
箱,则打折咖啡与原价牛奶共有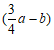 箱,
箱,
由题意得: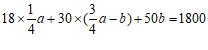 ,
,
整理得: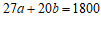 ,
,
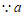 、
、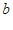 均为正整数,
均为正整数,
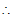
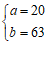 ,或
,或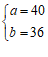 ,或
,或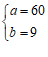 ,
,
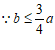 ,
,
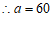 ,
,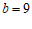 ,
,
即此次按原价采购的咖啡有9箱,
故答案为:9。
27. (5分)解:(1)x的取值范围是 -1<x<3 ;………………1分
x+y的取值范围是 -5<x+y<3 ;………2分
(2)∵x–y =a,∴x = a+y。
又∵x<–b,∴a+y<–b。
∴y<–a–b。
又∵y>2b,
∴2b< y<–a–b。 ……………………3分
∴a+b
<– y
<-2b。
①
∴2b+ a < y+ a <–b,
即 2b+ a < x <–b。
∴6b+3a< 3x<-3b。
②
①+②得7b+4a< 3x– y < -5b ……………4分
又∵-5<3x–y<5。
∴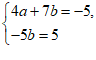
解得,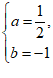
答:a的值是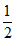 ,b的值是
,b的值是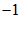 .………………5分
.………………5分
28. (6分)
(1)3,5;———–2分
(2)
①T<A,B,C,D,E,F,P,Q > =8,此时b<0,或0<b<4,或4<b<8,或b >8,
②T<A,B,C,D,E,F,P,Q > =6,此时b=4
②T<A,B,C,D,E,F,P,Q > =5,此时b=0,或b=8。
——-6分
(情况①完全正确给2分,b的取值范围不完整扣1分;情况②③各1分,b的取值范围不完整或者有错误不给分)